��Ŀ����
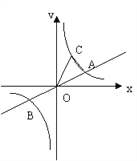
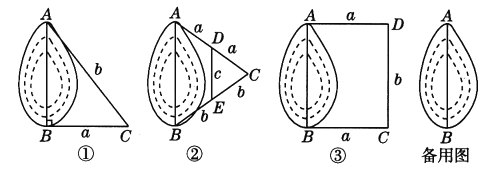
����Ŀ����ͼ��ʾ���ס�������ͬʱ�ɸۿ�A������������B���״��ض���������B���У����ٶ�Ϊ15����/Сʱ���Ҵ��ٶ�Ϊ20����/Сʱ����������������1Сʱ����C�ۿڽ��ÿͣ�ͣ����Сʱ����ת��ƫ��30�㷽����B�������ٶ���Ϊ20����/Сʱ��
��1����ۿ�A������B�ľ��룻
��2��B������һ�����������������Բ5�����ڶ����Կ����������ʼס���������һ���ȿ���������
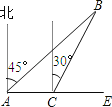
���𰸡���1���ۿ�A������B�ľ���Ϊ![]() �����2���Ҵ��ȿ���������
�����2���Ҵ��ȿ���������
��������
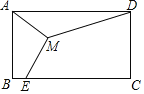
��1����BD��AE��D����������ֱ�������β��ý�ֱ����������BD��ʾ��CD��AD������DA��DC֮��Ĺ�ϵ�г�������⣮
��2���ֱ������������������ʱ�䣬Ȼ��Ƚϼ��ɣ�
��1������B��BD��AE��D
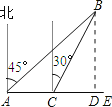
��Rt��BCD����BCD��60������CD��x����BD��![]() ��BC��2x
��BC��2x
��Rt��ABD����BAD��45��
��AD��BD��![]() ��AB��
��AB��![]() BD��
BD��![]()
��AC+CD��AD��20+x��![]()
��ã�x��10![]() +10
+10
��AB��30![]() +10
+10![]()
�𣺸ۿ�A������B�ľ���Ϊ![]() ���
���
��2���״�������������ʱ�䣺![]() ��4.1Сʱ
��4.1Сʱ
�Ҵ�������������ʱ�䣺![]() Сʱ
Сʱ
�����Ҵ��ȿ���������

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ