题目内容
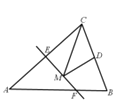
【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)求证:四边形ADEF是平行四边形;
(2)若∠ABC=60°,BD=6,求DE的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由BD是△ABC的角平分线,DE∥AB,可证得△BDE是等腰三角形,且BE=DE;又由BE=AF,可得DE=AF,即可证得四边形ADEF是平行四边形;
(2)过点E作EH⊥BD于点H,由∠ABC=60°,BD是∠ABC的平分线,可求得BH的长,从而求得BE、DE的长,即可求得答案.
(1)证明:∵BD是△ABC的角平分线,
∴∠ABD=∠DBE,
∵DE∥AB,
∴∠ABD=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE;
∵BE=AF,
∴AF=DE;
∴四边形ADEF是平行四边形;
(2)解:过点E作EH⊥BD于点H.
∵∠ABC=60°,BD是∠ABC的平分线,
∴∠ABD=∠EBD=30°,
∴DH=![]() BD=
BD=![]() ×6=3,
×6=3,
∵BE=DE,
∴BH=DH=3,
∴BE=![]() =
=![]() ,
,
∴DE=BE=![]() .
.

练习册系列答案
相关题目
【题目】某校兴趣小组在创客嘉年华活动中组织了计算机编程比赛,八年级每班派25名学生参加,成绩分别为![]() 、
、![]() 、
、![]() 、
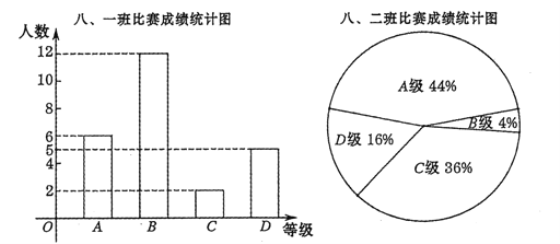
、![]() 四个等级.其中相应等级的得分依次记为10分、9分、8分、7分.将八年级的一班和二班的成绩整理并绘制成如下统计图表:
四个等级.其中相应等级的得分依次记为10分、9分、8分、7分.将八年级的一班和二班的成绩整理并绘制成如下统计图表:
班级 | 平均数(分) | 中位数(分) | 众数(分) | 方差 |
一班 | 8.76 | 9 | 9 |
|
二班 | 8.76 | 8 | 10 |
|
请根据本学期所学过的《数据的分析》相关知识分析上述数据,帮助计算机编程老师选择一个班级参加校级比赛,并阐述你选择的理由.