题目内容
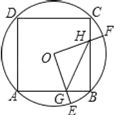
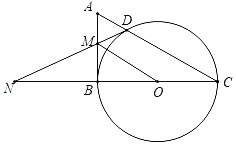
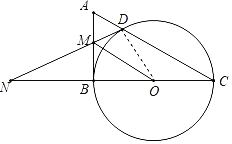
【题目】如图,在Rt△ABC中,以BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点M,交CB延长线于点N,连接OM,OC=1.
(1)求证:AM=MD;
(2)填空:
①若DN![]() ,则△ABC的面积为 ;
,则△ABC的面积为 ;
②当四边形COMD为平行四边形时,∠C的度数为 .
【答案】(1)详见解析;(2)①![]() ;②45°.
;②45°.
【解析】
(1)连接OD,根据切线的性质得到∠ODM=∠ABC=90°,根据全等三角形的判定定理得到Rt△BOM≌Rt△DOM(HL),求得BM=DM,∠DOM=∠BOM=![]() ∠DOB,根据圆周角定理得到∠BOM=∠C,于是得到结论;
∠DOB,根据圆周角定理得到∠BOM=∠C,于是得到结论;
(2)①由于tan∠DON=![]() ,求得∠DON=60°,根据圆周角定理得到
,求得∠DON=60°,根据圆周角定理得到![]() ,根据三角形的面积公式即可得到结论;
,根据三角形的面积公式即可得到结论;
②根据平行四边形的性质和圆周角定理即可得到结论.
(1)证明:连接OD,
∵DN为⊙O的切线,
∴∠ODM=∠ABC=90°,
在Rt△BOM与Rt△DOM中,
![]()
∴Rt△BOM≌Rt△DOM(HL),
∴BM=DM,∠DOM=∠BOM![]() ,
,
∵∠C![]() ,
,
∴∠BOM=∠C,
∴OM∥AC,
∵BO=OC,
∴BM=AM,
∴AM=DM;
(2)解:①∵OD=OC=1,DN![]() ,
,
∴tan∠DON![]() ,
,
∴∠DON=60°,
∴∠C=30°,
∵BC=2OC=2,
∴AB![]() BC
BC![]() ,
,
∴△ABC的面积为![]() ABBC
ABBC![]() 2
2![]() ;
;
②当四边形COMD为平行四边形时,∠C的度数为45°,
理由:∵四边形COMD为平行四边形,
∴DN∥BC,
∴∠DON=∠NDO=90°,
∴∠C![]() DON=45°.
DON=45°.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案【题目】在“全国爱眼日”这天,某校课题小组为了了解本校![]() 名学生的视力情况,随机抽查了部分学生的视力,并将调查的数据整理后绘制成如下的频率分布表和频数分布直方图(均不完整).
名学生的视力情况,随机抽查了部分学生的视力,并将调查的数据整理后绘制成如下的频率分布表和频数分布直方图(均不完整).
组别 | 视力 | 频率 |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
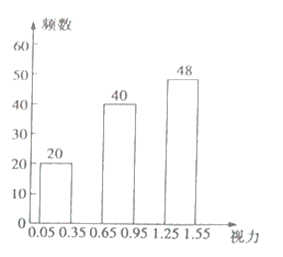
根据以上信息解答下列问题:
![]() 填空:
填空:![]() ______ _,并将频数分布直方图补充完整;
______ _,并将频数分布直方图补充完整;
![]() 若将统计结果绘制成扇形统计图,则第
若将统计结果绘制成扇形统计图,则第![]() 组所在扇形的圆心角度数为 ;
组所在扇形的圆心角度数为 ;
![]() 课题小组调查发现,每组中过度使用电子产品而造成视力下降的学生的比重如下表:
课题小组调查发现,每组中过度使用电子产品而造成视力下降的学生的比重如下表:
视力 |
|
|
|
|
|
比重 |
|
|
|
|
|
根据调查结果估计该校有多少名学生的视力下降是由于过度使用电子产品.