题目内容
已知四边形ABCD内接于圆，且弧AB、BC的度数分别为140°和100°，若弧AD=2•弧DC，则∠BCD=分析：圆的度数是360度，根据即可求得弧AD和弧DC的度数的和，再根据弧AD=2•弧DC即可求得弧CD的度数，根据圆周角定理即可求得
∠BCD的大小．
∠BCD的大小．
解答：解：弧AD和弧DC的度数的和=360-140-100=120°
又∵弧AD=2•弧DC
∴弧CD的度数是40°，弧AD=80°
∴弧BAD是140+80=220°
∴∠BCD=
×220=110°
故答案是：110°．
又∵弧AD=2•弧DC
∴弧CD的度数是40°，弧AD=80°
∴弧BAD是140+80=220°
∴∠BCD=
| 1 |
| 2 |
故答案是：110°．
点评：本题主要考查了圆的弧的度数的计算，以及圆周角的度数等于所对弧的度数的一半，是一个基础题．
练习册系列答案
互动课堂系列答案
相关题目
如图，已知四边形ABCD内接于直径为3的圆O，对角线AC是直径，对角线AC和BD的交点是P，AB=BD，且PC=0.6，求四边形ABCD的周长．
的延长线分别交于点F、E，且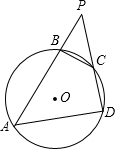
已知四边形ABCD内接于⊙O，分别延长AB和DC相交于点P，