题目内容
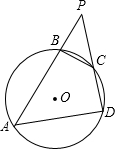已知四边形ABCD内接于⊙O，分别延长AB和DC相交于点P， |
| CB |
|
| CD |
分析：由切割线定理求出PC，证△PCB∽△PAD得到比例式求出AD，根据AD、AB、CD、BC的长度推出AC是直径，求出∠ABC=90°，根据勾股定理求出AC即可．
解答：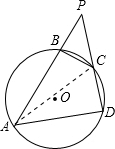
解：由切割线定理得：PB×PA=PC×PD，
∴8×（8+12）=PC×（PC+6），
∴PC=10，
连接AC，
∵四边形ABCD内接于圆O，
∴∠PCB=∠PAD，
∵∠P=∠P，
∴△PCB∽△PAD，
∴
=
，
∵弧BC=弧CD，
∴BC=CD=6，
∵PC=10，PA=8+12，
∴
=
，
∴AD=12=AB，
∴弧AB=弧AD，
∵弧BC=弧CD，
∴弧ABC=弧ADC，
∴AC是圆的直径，
∴∠ABC=90°，
由勾股定理得：AC=
=6
，
∴圆O的半径是3
，面积是π•(3
)2=45π，
故答案为：45π．
解：由切割线定理得：PB×PA=PC×PD，∴8×（8+12）=PC×（PC+6），
∴PC=10，
连接AC，
∵四边形ABCD内接于圆O，
∴∠PCB=∠PAD，
∵∠P=∠P，
∴△PCB∽△PAD，
∴
| PC |
| PA |
| BC |
| AD |
∵弧BC=弧CD，
∴BC=CD=6，
∵PC=10，PA=8+12，
∴
| 10 |
| 8+12 |
| 6 |
| AD |
∴AD=12=AB，
∴弧AB=弧AD，
∵弧BC=弧CD，
∴弧ABC=弧ADC，
∴AC是圆的直径，
∴∠ABC=90°，
由勾股定理得：AC=
| AB2+BC2 |
| 5 |
∴圆O的半径是3
| 5 |
| 5 |
故答案为：45π．
点评：本题主要考查对圆周角定理，勾股定理，相似三角形的性质和判定等知识点的连接和掌握，能推出AC是直径是解此题的关键．
练习册系列答案
相关题目
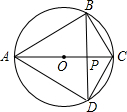如图，已知四边形ABCD内接于直径为3的圆O，对角线AC是直径，对角线AC和BD的交点是P，AB=BD，且PC=0.6，求四边形ABCD的周长．
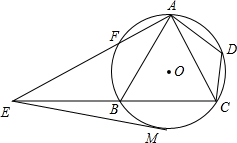的延长线分别交于点F、E，且