题目内容
【题目】列方程(组)及不等式解应用题
某种型号油、电混合动力汽车,从A地到B地使用纯燃油行驶的费用为76元;从A地到B地使用纯电行驶的费用为26元.已知每行驶1千米用纯燃油行驶的费用比用纯电行驶的费用多0.5元.
(1)求用纯电行驶1千米的费用为多少元?
(2)若要使从A地到B地油电混合行驶所需的油和电总费用不超过39元,则至少用电行驶多少千米?
【答案】(1)用纯电行驶1千米的费用为0.26元;(2)至少用电行驶74千米.
【解析】
(1)根据题意找出等量关系,列出相应的分式方程,然后解方程求解即可;(2)根据(1)中用电每千米的费用和(2)中的信息列出相应的不等式,解不等式即可求解.
(1)设用纯电行驶1千米的费用为x元,则用纯油行驶1千米的费用为(x+0.5)元,
根据题意得:![]() ,
,
解得:x=0.26,
经检验,x=0.26是原分式方程的解.
答:用纯电行驶1千米的费用为0.26元.
(2)设从A地到B地用电行驶y千米,
根据题意得:0.26y+(0.26+0.5)(![]() ﹣y)≤39,
﹣y)≤39,
解得:y≥74.
答:至少用电行驶74千米.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
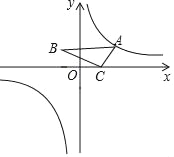
小学课时特训系列答案【题目】(本题12分)某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球运行时,设乒乓球与端点A的水平距离为![]() (米),与桌面的高度为
(米),与桌面的高度为![]() (米),运行时间为
(米),运行时间为![]() (秒),经多次测试后,得到如下部分数据:
(秒),经多次测试后,得到如下部分数据:
| 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0. 8 | … |
| 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
| 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
(1)当![]() 为何值时,乒乓球达到最大高度?
为何值时,乒乓球达到最大高度?
(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后,![]() 与
与![]() 满足
满足![]()
①用含![]() 的代数式表示
的代数式表示![]() ;
;
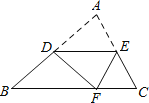
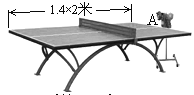
②球网高度为0.14米,球桌长(1.4×2)米,若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A,求![]() 的值.
的值.