Question

【题目】一个正六边形和两个等边三角形的位置如图所示,∠3=70°，则∠1+∠2=__

Answer 1

【答案】50°

【解析】

先在∠1、∠3、∠2的顶点分别标上字母A、B、C.根据正六边形及正三角形的性质用∠1表示出∠BAC，用∠2表示出∠ACB，用∠3表示出∠ABC，再由三角形内角和定理即可得出结论．

解：如图，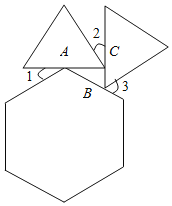

∵图中是一个正六边形和两个等边三角形，
∴∠BAC=180°-∠1-120°=60°-∠1，

∠ACB=180°-∠2-60°=120°-∠2，

∠ABC=180°-60°-∠3=120°-∠3，
∵∠3=70°，
∴∠ABC=180°-60°-∠3=120°-70°=50°．
∵∠BAC+∠ACB+∠ABC=180°，

即60°-∠1+120°-∠2+50°=180°，
∴∠1+∠2=50°．
故答案是：50°．