题目内容
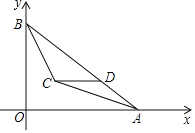
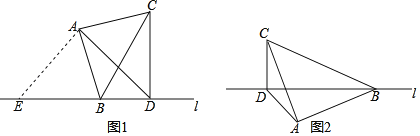
【题目】如图1,点B在直线l上,过点B构建等腰直角三角形ABC,使∠BAC=90°,且AB=AC,过点C作CD⊥直线l于点D,连接AD.
(1)小亮在研究这个图形时发现,∠BAC=∠BDC=90°,点A,D应该在以BC为直径的圆上,则∠ADB的度数为 °,将射线AD顺时针旋转90°交直线l于点E,可求出线段AD,BD,CD的数量关系为 ;
(2)小亮将等腰直角三角形ABC绕点B在平面内旋转,当旋转到图2位置时,线段AD,BD,CD的数量关系是否变化,请说明理由;
(3)在旋转过程中,若CD长为1,当△ABD面积取得最大值时,请直接写AD的长.
【答案】(1)45°,CD+DB=![]() AD;(2)线段AD,BD,CD的数量关系会变化,数量关系为BD﹣CD=
AD;(2)线段AD,BD,CD的数量关系会变化,数量关系为BD﹣CD=![]() AD.证明见解析;(3)1+
AD.证明见解析;(3)1+![]() .
.
【解析】
(1)由∠BAC=90°,且AB=AC,可得∠ACB=∠ABC=45°,由∠BAC=∠BDC=90°,推出A、B、C、D四点共圆,所以∠ADB=∠ACB=45°;由题意知△EAB≌△DAC,所以BE=CD,由AE=AD,∠EAD=90°,可知△ADE是等腰直角三角形,推出CD+DB=EB+BD=DE=![]() AD;
AD;
(2)如图2,将AD绕点A顺时针旋转90°交直线l于点E.易证△EAB≌△DAC(SAS),则BE=CD,由AE=AD,∠EAD=90°,所以△ADE是等腰直角三角形,则DE=![]() AD,由BDCD=BDBE=DE,推出BDCD=
AD,由BDCD=BDBE=DE,推出BDCD=![]() AD;
AD;
(3)当点D在线段AB的垂直平分线上且在AB的左侧时,△ABD的面积最大,据此即可求解.
解:(1)①如图,在图1中.
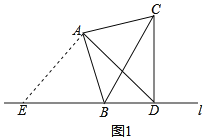
∵∠BAC=90°,且AB=AC,
∴∠ACB=∠ABC=45°,
∵∠BAC=∠BDC=90°,
∴A、B、C、D四点共圆,
∴∠ADB=∠ACB=45°;
②由题意可知,∠EAD=∠BAC=90°,
∴∠EAB=∠DAC,
又AE=AD,AB=AC,
∴△EAB≌△DAC(SAS),
∴BE=CD,
∵AE=AD,∠EAD=90°,
∴△ADE是等腰直角三角形,
∴DE=![]() =
=![]() AD,
AD,
∵CD+DB=EB+BD=DE,
∴CD+DB=![]() AD;
AD;
故答案为45°;CD+DB=![]() AD;
AD;
(2)线段AD,BD,CD的数量关系会变化,数量关系为BD﹣CD=![]() A.
A.
理由如下:
如图2,将AD绕点A顺时针旋转90°交直线l于点E.
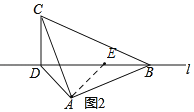
则∠DAE=∠CAB=90°,
∴∠DAC=∠EAB,
又AD=AE,AC=AB,
∴△EAB≌△DAC(SAS),
∴BE=CD,
∵AE=AD,∠EAD=90°,
∴△ADE是等腰直角三角形,
∴DE=![]() =
=![]() AD,
AD,
∵BD﹣CD=BD﹣BE=DE,
∴BD﹣CD=![]() AD;
AD;
(3)由(2)知,△CDA≌△BEA,
∴∠CDA=∠AEB,
∵∠DEA=45°,
∴∠AEB=180°﹣45°=135°,
∴∠CDA=∠AEB=135°,
∴∠CDA+∠ABC=135°+45°=180°,
∴A、B、C、D四点共圆,
于是作A、B、C、D外接圆⊙O,如图3.
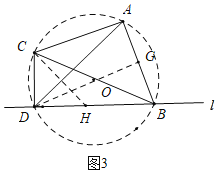
当点D在线段AB的垂直平分线上且在AB的左侧时,△ABD的面积最大.
作DG⊥AB,则DG平分∠ADB,DB=DA,在DA上截取一点H,使得CD=DH=1,
∵∠ADB=∠ACB=45°,
∴∠GDB=22.5°,∠DBG=67.5°,
∴∠DBC=67.5°﹣45°=22.5°,
∠HCB=∠DHC﹣∠HBC=45°﹣22.5°=22.5°,
∴∠HCB=∠HBC,
∴HB=CH=![]() =
=![]() ,
,
∴AD=BD=DH+BH=1+![]() .
.