题目内容
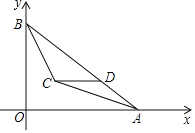
【题目】如图，平面直角坐标系中，A（8，0），B（0，6），∠BAO，∠ABO的平分线相交于点C，过点C作CD∥x轴交AB于点D，则点D的坐标为（ ）
A.（ 
，2）B.（ ，1）C.（ 
，2）D.（，1）
【答案】A
【解析】
延长DC交y轴于F，过C作CG⊥OA于G，CE⊥AB于E，根据角平分线的性质得到FC＝CG＝CE，求得DH＝CG＝CF，设DH＝3x，AH＝4x，根据勾股定理得到AD＝5x，根据平行线的性质得到∠DCA＝∠CAG，求得∠DCA＝∠DAC，得到CD＝HG＝AD＝5x，列方程即可得到结论．
解：延长DC交y轴于F，过C作CG⊥OA于G，CE⊥AB于E，
∵CD∥x轴，
∴DF⊥OB，
∵∠BAO，∠ABO的平分线相交于点C，
∴FC＝CG＝CE，
∴DH＝CG＝CF，
∵A（8，0），B（0，6），
∴OA＝8，OB＝6，
∴tan∠OAB＝
＝
＝
，
∴设DH＝3x，AH＝4x，
∴AD＝5x，
∵CD∥OA，
∴∠DCA＝∠CAG，
∵∠DAC＝∠GAC，
∴∠DCA＝∠DAC，
∴CD＝HG＝AD＝5x，
∴3x+5x+4x＝8，
∴x＝
，
∴DH＝2，OH＝
，
∴D（，2），
故选：A．
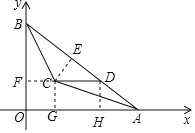
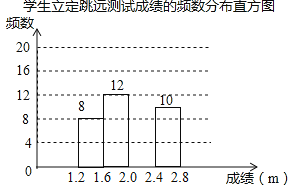
【题目】为了解某校九年级学生立定跳远水平，随机抽取该年级50名学生进行测试，并把测试成绩（单位：m）绘制成不完整的频数分布表和频数分布直方图．
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x＜1.6 | a |
1.6≤x＜2.0 | 12 |
2.0≤x＜2.4 | b |
2.4≤x＜2.8 | 10 |
请根据图表中所提供的信息，完成下列问题：
（1）表中a= ，b= ，样本成绩的中位数落在 范围内；
（2）请把频数分布直方图补充完整；
（3）该校九年级共有1000名学生，估计该年级学生立定跳远成绩在2.4≤x＜2.8范围内的学生有多少人？
