题目内容
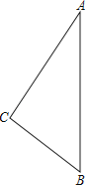
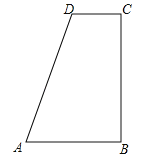
【题目】如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.
(1)利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法);
(2)在(1)的条件下,①证明:AE⊥DE;
②若CD=2,AB=4,点M,N分别是AE,AB上的动点,求BM+MN的最小值.
【答案】(1)答案见解析;(2)①证明见解析;②![]() .
.
【解析】
(1)利用尺规作出∠ADC的角平分线即可;
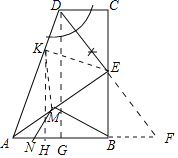
(2)①延长DE交AB的延长线于F.只要证明AD=AF,DE=EF,利用等腰三角形三线合一的性质即可解决问题;②作点B关于AE的对称点K,连接EK,作KH⊥AB于H,DG⊥AB于G.连接MK.由MB=MK,推出MB+MN=KM+MN,根据垂线段最短可知:当K、M、N共线,且与KH重合时,KM+MN的值最小,最小值为KH的长.
(1)如图,∠ADC的平分线DE如图所示,
(2)延长DE交AB的延长线于F,
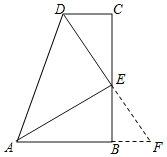
∵CD∥AF,
∴∠CDE=∠F,
∵∠CDE=∠ADE,
∴∠ADF=∠F,
∴AD=AF,
∵AD=AB+CD=AB+BF,
∴CD=BF,
∵∠DEC=∠BEF,
∴△DEC≌△FEB,
∴DE=EF,
∵AD=AF,
∴AE⊥DE;
②作点B关于AE的对称点K,连接EK,作KH⊥AB于H,DG⊥AB于G.连接MK,
∵AD=AF,DE=EF,
∴AE平分∠DAF,则△AEK≌△AEB,
∴AK=AB=4,
在Rt△ADG中,DG![]() ,
,
∵KH∥DG,
∴![]() ,
,
∴![]() ,
,
∴KH![]() ,
,
∵MB=MK,
∴MB+MN=KM+MN,
∴当K、M、N共线,且与KH重合时,KM+MN的值最小,最小值为KH的长,∴BM+MN的最小值为![]() .
.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目