题目内容
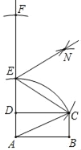
【题目】如图,已知矩形ABCD,按照下列操作作图:①以A为圆心,AC长为半径画弧交AD的延长线于点E;②以E为圆心,EC长为半径画弧交DE的延长线于点F;③分别以C,F为圆心,大于![]() CF的长为半径画弧,两弧相交于点N;④作射线EN,根据作图,若∠ACB=72°,则∠FEN的度数为( )
CF的长为半径画弧,两弧相交于点N;④作射线EN,根据作图,若∠ACB=72°,则∠FEN的度数为( )
A. 54° B. 63° C. 72° D. 75°
【答案】B
【解析】
由题意可得AE=AC,△AEC为等腰三角形,∠CAE=∠ACB=72°,可得△FEN≌△CEN,∠FEN= ∠CEN可得∠FEN的度数.
解:由题意得:AE=AC,![]() △AEC为等腰三角形,
△AEC为等腰三角形,
![]() ∠ACB=72°,四边形ABCD为矩形,
∠ACB=72°,四边形ABCD为矩形, ![]() ∠CAE=72°, ∠CEA=
∠CAE=72°, ∠CEA=![]() =54
=54![]() ,
,
由以E为圆心,EC长为半径画弧交DE的延长线于点F;分别以C,F为圆心,大于![]() CF的长为半径画弧,两弧相交于点N,可得EF=CE,FN=CN,又
CF的长为半径画弧,两弧相交于点N,可得EF=CE,FN=CN,又![]() EN=EN,
EN=EN,
![]() △FEN≌△CEN,
△FEN≌△CEN,
![]() ∠FEN= ∠CEN
∠FEN= ∠CEN
![]() ∠FEN=
∠FEN=![]() =63
=63![]()
故选B.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目