题目内容
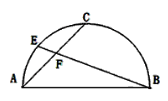
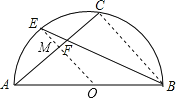
【题目】如图,AB是半圆的直径,点C是弧AB的中点,点E是弧AC的中点,连结EB、CA交于点F,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
先连接OE、BC,利用垂径定理推论,以及圆心角、弧、弦之间的关系,可证得:△ABC、△AMO是等腰直角三角形且OE∥BC,再证△MEF∽△CBF,利用相似三角形的性质即可求出.
解:取AB中点O,连接OE、BC,OE与AC交于点M.
∵AB是半圆的直径, 点C是弧AB的中点,
∴∠ACB=90°,则△ABC是等腰直角三角形,
∵E为弧AC的中点,
∴OE⊥AC,AM=MC,∠AOE=45°,
∴OE∥BC,△AMO是等腰直角三角形,
设OM=1,则AM=1,
∴AC=BC=2,OA=![]() ,
,
∴OE=![]() ,
,
∴EM=![]()
∵OE∥BC,
∴△MEF∽△CBF,
∴![]() ,
,
故选D.

练习册系列答案
相关题目