题目内容
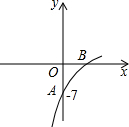 已知抛物线y=(1-a)x2+8x+b的图象的一部分如图所示,抛物的顶点在第一象限,且经过点A(0,-7)和点B.
已知抛物线y=(1-a)x2+8x+b的图象的一部分如图所示,抛物的顶点在第一象限,且经过点A(0,-7)和点B.(1)求a的取值范围;
(2)若OA=2OB,求抛物线的解析式.
分析:(1)因为二次函数过点A,所以可以确定b的值,又因为抛物线为y=(1-a)x2+8x-7又抛物线的顶点在第一象限,开口向下,所以抛物线与x轴有两个不同的交点,所以可以确定1-a<0,△>0,解不等式组即可求得a的取值范围;
(2)因为OA=2OB,可求得点B的坐标,将点A,B的坐标代入二次函数的解析式即可求得a,b的值,即可求得二次函数的解析式.
(2)因为OA=2OB,可求得点B的坐标,将点A,B的坐标代入二次函数的解析式即可求得a,b的值,即可求得二次函数的解析式.
解答:解:(1)由图可知,b=-7.(1分)
故抛物线为y=(1-a)x2+8x-7.
又因抛物线的顶点在第一象限,开口向下,
所以抛物线与x轴有两个不同的交点.
∴
,
解之,得1<a<
.(3分)
即a的取值范围是1<a<
.(6分)
(2)设B(x1,0),
由OA=20B,
得7=2x1,即x1=
.(7分)
由于x1=
,方程(1-a)x2+8x-7=0的一个根,
∴(1-a)(
)2+8×
-7=0
∴a=
.(9分)
故所求所抛物线解析式为y=-
x2+8x-7.(10分)
故抛物线为y=(1-a)x2+8x-7.
又因抛物线的顶点在第一象限,开口向下,
所以抛物线与x轴有两个不同的交点.
∴
|
解之,得1<a<
| 23 |
| 7 |
即a的取值范围是1<a<
| 23 |
| 7 |
(2)设B(x1,0),
由OA=20B,
得7=2x1,即x1=
| 7 |
| 2 |
由于x1=
| 7 |
| 2 |
∴(1-a)(
| 7 |
| 2 |
| 7 |
| 2 |
∴a=
| 19 |
| 7 |
故所求所抛物线解析式为y=-
| 12 |
| 7 |
点评:此题考查了二次函数的图象的性质,开口方向,与x轴的交点个数与△的关系,待定系数法求函数解析式等;
解题的关键是数形结合思想的应用.
解题的关键是数形结合思想的应用.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
 正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为
正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为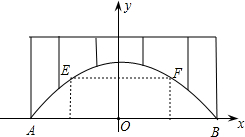 廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-
廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-