题目内容
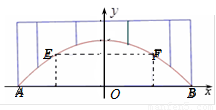
 廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-
廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-| 1 | 40 |
分析:已知抛物线上距水面AB高为8米的E、F两点,可知E、F两点纵坐标为8,把y=8代入抛物线解析式,可求E、F两点的横坐标,根据抛物线的对称性求EF长.
解答:解:由于两盏E、F距离水面都是8m,因而两盏景观灯之间的水平距离就
是直线y=8与抛物线两交点的横坐标差的绝对值.
故有-
x2+10=8,
即x2=80,x1=4
,x2=-4
.
所以两盏警示灯之间的水平距离为:
|x1-x2|=|4
-(-4
)|=8
≈18(m)
是直线y=8与抛物线两交点的横坐标差的绝对值.
故有-
| 1 |
| 40 |
即x2=80,x1=4
| 5 |
| 5 |
所以两盏警示灯之间的水平距离为:
|x1-x2|=|4
| 5 |
| 5 |
| 5 |
点评:本题考查的是二次函数在实际生活中的应用,比较简单.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
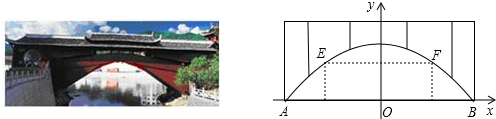
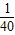 x2+10,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是 米.(精确到1米)
x2+10,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是 米.(精确到1米)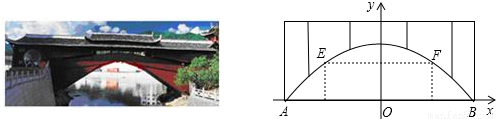
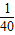 x2+10,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是 米.(精确到1米)
x2+10,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,则这两盏灯的水平距离EF是 米.(精确到1米)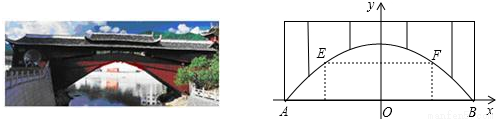
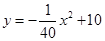 ,为保护廊桥的安全,在该抛物线上距水面
,为保护廊桥的安全,在该抛物线上距水面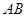 高为8米的点、处要安装两盏警示灯,则这两盏灯的水平距离
高为8米的点、处要安装两盏警示灯,则这两盏灯的水平距离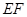 是
(精确到1米)
是
(精确到1米)