题目内容
已知抛物线经过点A(1,0)、B(2,-3)、C(0,4)三点.(1)求此抛物线的解析式;
(2)如果点D在这条抛物线上,点D关于这条抛物线对称轴的对称点是点C,求点D的坐标.
分析:(1)用待定系数法,把A,B,C三点的坐标代入,解答出即可;
(2)求出抛物线的对称轴,根据对称的性质,即可求出点D的坐标;
(2)求出抛物线的对称轴,根据对称的性质,即可求出点D的坐标;
解答:解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
则
,
解得
.
∴抛物线的解析式为y=
x2-
x+4;
(2)∵抛物线的对称轴为直线x=
,且点D,C关于对称轴对称,
∴点D的坐标为(9,4).
则
|
解得
|
∴抛物线的解析式为y=
| 1 |
| 2 |
| 9 |
| 2 |
(2)∵抛物线的对称轴为直线x=
| 9 |
| 2 |
∴点D的坐标为(9,4).
点评:本题主要考查了待定系数法求二次函数的解析式和对称的性质,要会利用数形结合的思想把代数和几何图形结合起来.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
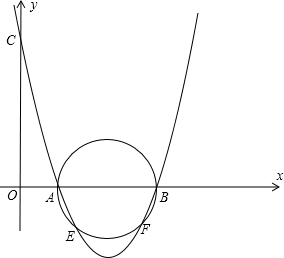 已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆.
已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆. 如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点.
如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点.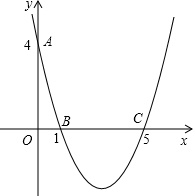 如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.
如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.