题目内容
已知抛物线y=ax2+bx+c(a≠0)与x轴交于不同的两点A(x1,0)和B(x2,0),与y轴的 正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为
正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为| 15 | 2 |
(1)求此抛物线的解析式;
(2)求直线AC和BC的方程;
(3)如果P是线段AC上的一个动点(不与点A、C重合),过点P作直线y=m(m为常数),与直线BC交于点Q,则在x轴上是否存在点R,使得△PQR为等腰直角三角形?若存在,求出点R的坐标;若不存在,请说明理由.
分析:(1)已知A,B的坐标,易求出三角形ABC的面积以及点C的坐标.易求解析式.
(2)已知A,B,C三点的坐标,易求AC,BC的方程式.
(3)假设存在点R,直线y=m与y轴的交点为点E.证明点P不与点O,C重合,证明△CPQ∽△CAB后解得P,Q的坐标.
(2)已知A,B,C三点的坐标,易求AC,BC的方程式.
(3)假设存在点R,直线y=m与y轴的交点为点E.证明点P不与点O,C重合,证明△CPQ∽△CAB后解得P,Q的坐标.
解答: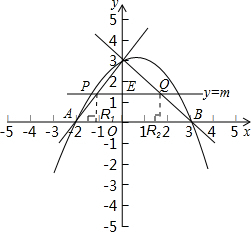 解:(1)A(-2,O),B(3,0),
解:(1)A(-2,O),B(3,0),
S△ABC=
,
∴c=3,C(0,3).
∴抛物线的解析式是y=-
x2+
x+3.
(2)由(1)可知,直线AC的方程为y=
+3,直线BC的方程为y=-x+3.
(3)假设存在满足条件的点R,并设直线y=m与y轴的交点为E(0,m),
由(1),知AB=5,OC=3.
点P不与点A、C重合,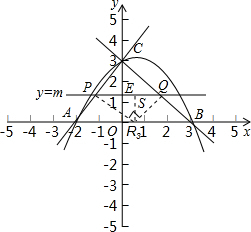
∴点E(0,m)不与点O、C重合.
∴0<m<3.
由于PQ为等腰直角三角形加PQR的一腰,
过点P作PR1⊥x轴于点R1,则∠R1PQ=90°,PQ=PR1=m.
即(3-m)-
=m,
解得m=
.
∴P(xP,
),Q(xQ,
),
点P在直线AC上,
解得xP=-
,P(-
,
).
∴点R1(-
,0).
过点Q作QR2⊥x轴于R2,
同理可求得xQ=
,Q(
,
).
∴点R2(
,0).验证成立,
当∠PRQ=90°时,PQ=2m,即(3-m)-
=2m,
解得m=
,此时R的横坐标为
[(3-m)+
]=
,
∴R1(-
,0)、R2(
,0)、R3(
,0)是满足条件的点.
 解:(1)A(-2,O),B(3,0),
解:(1)A(-2,O),B(3,0),S△ABC=
| 15 |
| 2 |
∴c=3,C(0,3).
∴抛物线的解析式是y=-
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)可知,直线AC的方程为y=
| 3x |
| 2 |
(3)假设存在满足条件的点R,并设直线y=m与y轴的交点为E(0,m),
由(1),知AB=5,OC=3.
点P不与点A、C重合,

∴点E(0,m)不与点O、C重合.
∴0<m<3.
由于PQ为等腰直角三角形加PQR的一腰,
过点P作PR1⊥x轴于点R1,则∠R1PQ=90°,PQ=PR1=m.
即(3-m)-
| 2m-6 |
| 3 |
解得m=
| 15 |
| 8 |
∴P(xP,
| 15 |
| 8 |
| 15 |
| 8 |
点P在直线AC上,
解得xP=-
| 3 |
| 4 |
| 3 |
| 4 |
| 15 |
| 8 |
∴点R1(-
| 3 |
| 4 |
过点Q作QR2⊥x轴于R2,
同理可求得xQ=
| 9 |
| 8 |
| 9 |
| 8 |
| 15 |
| 8 |
∴点R2(
| 9 |
| 8 |
当∠PRQ=90°时,PQ=2m,即(3-m)-
| 2m-6 |
| 3 |
解得m=
| 15 |
| 11 |
| 1 |
| 2 |
| 2m-6 |
| 3 |
| 3 |
| 11 |
∴R1(-
| 3 |
| 4 |
| 9 |
| 8 |
| 3 |
| 11 |
点评:本题考查的是二次函数的综合运用,要利用大量的辅助线的帮助,难度较大.

练习册系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=