题目内容
(2013•广州)已知抛物线y1=ax2+bx+c(a≠0,a≠c)过点A(1,0),顶点为B,且抛物线不经过第三象限.
(1)使用a、c表示b;
(2)判断点B所在象限,并说明理由;
(3)若直线y2=2x+m经过点B,且于该抛物线交于另一点C(
,b+8),求当x≥1时y1的取值范围.
(1)使用a、c表示b;
(2)判断点B所在象限,并说明理由;
(3)若直线y2=2x+m经过点B,且于该抛物线交于另一点C(
| c | a |
分析:(1)抛物线经过A(1,0),把点代入函数即可得到b=-a-c;
(2)判断点在哪个象限,需要根据题意画图,由条件:图象不经过第三象限就可以推出开口向上,a>0,只需要知道抛物线与x轴有几个交点即可解决,
判断与x轴有两个交点,一个可以考虑△,由△就可以判断出与x轴有两个交点,所以在第四象限;或者直接用公式法(或十字相乘法)算出,由两个不同的解x1=1,x2=
,(a≠c),进而得出点B所在象限;
(3)当x≥1时,y1的取值范围,只要把图象画出来就清晰了,难点在于要观察出C(
,b+8)是抛物线与x轴的另一个交点,理由是x1=1,x2=
,(a≠c),由这里可以发现,b+8=0,b=-8,a+c=8,还可以发现C在A的右侧;可以确定直线经过B、C两点,看图象可以得到,x≥1时,y1大于等于最小值,此时算出二次函数最小值即可,即求出
即可,已经知道b=-8,a+c=8,算出a,c即可,即可得出y1的取值范围.
(2)判断点在哪个象限,需要根据题意画图,由条件:图象不经过第三象限就可以推出开口向上,a>0,只需要知道抛物线与x轴有几个交点即可解决,
判断与x轴有两个交点,一个可以考虑△,由△就可以判断出与x轴有两个交点,所以在第四象限;或者直接用公式法(或十字相乘法)算出,由两个不同的解x1=1,x2=
| c |
| a |
(3)当x≥1时,y1的取值范围,只要把图象画出来就清晰了,难点在于要观察出C(
| c |
| a |
| c |
| a |
| 4ac-b2 |
| 4a |
解答: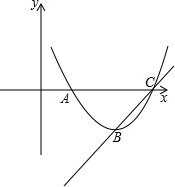 解:(1)∵抛物线y1=ax2+bx+c(a≠0,a≠c),经过A(1,0),
解:(1)∵抛物线y1=ax2+bx+c(a≠0,a≠c),经过A(1,0),
把点代入函数即可得到:b=-a-c;
(2)B在第四象限.
理由如下:∵抛物线y1=ax2+bx+c(a≠0,a≠c)过点A(1,0),
∵x1•x2=
,
∴x1=1,x2=
,a≠c,
所以抛物线与x轴有两个交点,
又因为抛物线不经过第三象限,
所以a>0,且顶点在第四象限;
(3)∵C(
,b+8),且在抛物线上,
∴b+8=0,∴b=-8,
∵a+c=-b,∴a+c=8,
把B(-
,
)、C(
,b+8)两点代入直线解析式得:
,
解得:
或
(a≠c,舍去)
如图所示,C在A的右侧,
∴当x≥1时,y1≥
=-2.
 解:(1)∵抛物线y1=ax2+bx+c(a≠0,a≠c),经过A(1,0),
解:(1)∵抛物线y1=ax2+bx+c(a≠0,a≠c),经过A(1,0),把点代入函数即可得到:b=-a-c;
(2)B在第四象限.
理由如下:∵抛物线y1=ax2+bx+c(a≠0,a≠c)过点A(1,0),
∵x1•x2=
| c |
| a |
∴x1=1,x2=
| c |
| a |
所以抛物线与x轴有两个交点,
又因为抛物线不经过第三象限,
所以a>0,且顶点在第四象限;
(3)∵C(
| c |
| a |
∴b+8=0,∴b=-8,
∵a+c=-b,∴a+c=8,
把B(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
| c |
| a |
|
解得:
|
|
如图所示,C在A的右侧,
∴当x≥1时,y1≥
| 4ac-b2 |
| 4a |
点评:此题主要考查了二次函数的综合应用以及根与系数的关系和一次函数与二次函数交点问题等知识,根据数形结合得出是解题关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
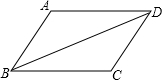 (2013•广州)已知四边形ABCD是平行四边形(如图),把△ABD沿对角线BD翻折180°得到△A′BD.
(2013•广州)已知四边形ABCD是平行四边形(如图),把△ABD沿对角线BD翻折180°得到△A′BD. (2013•广州)如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里.
(2013•广州)如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里.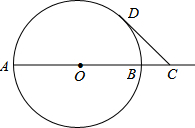 (2013•广州)已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.
(2013•广州)已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.