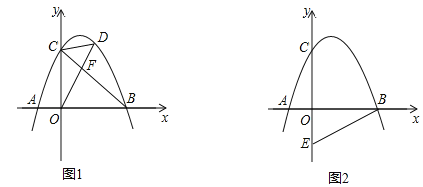题目内容
【题目】在平面直角坐标系中,抛物线y=ax2+bx+![]() 与x轴分别交于点A(﹣1,0),B(3,0),点C是顶点.
与x轴分别交于点A(﹣1,0),B(3,0),点C是顶点.
(1)求抛物线的解析式;
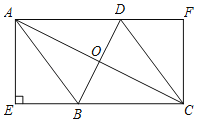
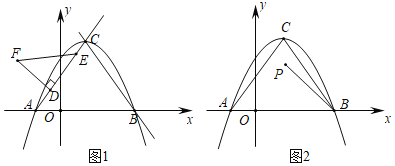
(2)如图1,线段DE是射线AC上的一条动线段(点D在点E的下方),且DE=2,点D从点A出发沿着射线AC的方向以每秒2个单位长度的速度运动,以DE为一边在AC上方作等腰Rt△DEF,其中∠EDF=90°,设运动时间为t秒.
①点D的坐标是 (用含t的代数式表示);
②当直线BC与△DEF有交点时,请求出t的取值范围;
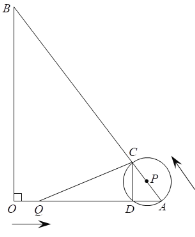
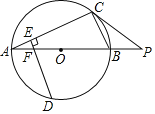
(3)如图2,点P是△ABC内一动点,BP=![]() ,点M,N分别是AB,BC边上的两个动点,当△PMN的周长最小时,请直接写出四边形PNBM面积的最大值.
,点M,N分别是AB,BC边上的两个动点,当△PMN的周长最小时,请直接写出四边形PNBM面积的最大值.
【答案】(1)y=﹣![]() x2+
x2+![]() x+
x+![]() ;(2)①(t﹣1,
;(2)①(t﹣1,![]() t);②1≤t≤
t);②1≤t≤![]() ﹣
﹣![]() ;(3)
;(3)![]() .
.
【解析】
(1)直接利用待定系数法,建立方程组求解即可得出结论;
(2)先判断出△ABC是等边三角形,
①利用三角函数表示出AQ,DQ,即可得出结论;
②先表示出点E,F的坐标,再求出直线BC的解析式,点E,F代入直线BC的解析式中,即可求出分界点,即可得出结论;
(3)先判断出△BEF是要为BP,顶角为120°的等腰三角形,进而求出△BEF的面积,再判断出四边形PNBM的面积最大,得出△BMN的面积最小,此时,BP⊥EF,即可得出结论.
(1)∵抛物线y=ax2+bx+![]() 与x轴分别交于点A(﹣1,0),B(3,0),
与x轴分别交于点A(﹣1,0),B(3,0),
∴ ,
,
∴ ,
,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+
x+![]() ;
;
(2)如图1,
由(1)知,抛物线的解析式为y=﹣![]() x2+
x2+![]() x+
x+![]() =﹣
=﹣![]() (x﹣1)2+2
(x﹣1)2+2![]() ,
,
∴点C(1,2![]() ),
),
∵A(﹣1,0),
∵A(﹣1,0),B(3,0),
∴AB=4,AC=![]() =4,BC=
=4,BC=![]() =4,
=4,
∴AB=AC=BC,
∴△ABC是等边三角形,
∴∠BAC=60°,
①过点D作DQ⊥AB于Q,
由运动知,AD=2t,
∴AQ=t,
∴DQ=![]() t,
t,
∴D(t﹣1,![]() t),
t),
故答案为:(t﹣1,![]() t);
t);
②过点F作AB的垂线,交过点D平行于AB的直线于G,
∴∠FDG=60°,
∵∠ADF=90°,
∴∠FDG=30°,
∴FG=![]() DF=
DF=![]() DE=1,DG=
DE=1,DG=![]() ,
,
∴F(t﹣1﹣1,![]() t+1),E(t﹣1+1,
t+1),E(t﹣1+1,![]() t+
t+![]() ),
),
即F(t﹣2,![]() t+1),E(t,
t+1),E(t,![]() t+
t+![]() ),
),
∵点B(3,0),C(1,2![]() ),
),
∴直线BC的解析式为y=﹣![]() x+3
x+3![]() ,
,
当点E在直线BC上时,﹣![]() t+3
t+3![]() =
=![]() t+
t+![]() ,
,
∴t=1,
当点F在直线BC上时,﹣![]() (t﹣2)+3
(t﹣2)+3![]() =
=![]() t+1,
t+1,
∴t=![]() ﹣
﹣![]() ,
,
即当直线BC与△DEF有交点时,t的取值范围为1≤t≤![]() ﹣
﹣![]() ;
;
(3)如图2,
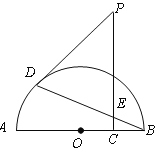
作点P关于AB的对称点F,作点P关于BC的对称点E,连接EF,交AB于M,交BC于N,连接PM,PN,
则△PMN的周长最小为PM+PN+MN=FM+EN+MN=EF,
由对称性知,BE=BF=BP=![]() ,∠EBN=∠PBN,∠FBM=∠PBM,
,∠EBN=∠PBN,∠FBM=∠PBM,
∴∠EBN=∠EBN+∠PBN+∠FBM+∠PBM=2(∠PBN+∠PBM)=2∠ABC=120°,
∴∠BFE=30°,
过点B作BH⊥EF于H,则EF=2FH,
在Rt△BHM中,BH=![]() BF=
BF=![]() ,FH=
,FH=![]() ,
,
∴EF=2FH=![]() ,
,
∴S△BEF=![]() EFBH=
EFBH=![]() ,
,
∵S四边形PNBM=![]() (S△BEF+S△PMN)=
(S△BEF+S△PMN)=![]() (
(![]() +S△PMN),
+S△PMN),
要使四边形PNBM的面积最大,则△PMN的面积最大,即△BMN的的面积最小,
只有BP⊥EF时,△BMN的面积最小,此时,MN=2×![]() =
=![]() ,PH=BP﹣BH=
,PH=BP﹣BH=![]() ﹣
﹣![]() =
=![]() ,
,
∴S△PMN最大=![]() MNPH=
MNPH=![]() ,
,
即S四边形PNBM最大=![]() (S△BEF+S△PMN)=
(S△BEF+S△PMN)=![]() (
(![]() +
+![]() )=
)=![]() ,
,
∴当△PMN的周长最小时,四边形PNBM面积的最大值为![]() .
.



 阅读快车系列答案
阅读快车系列答案【题目】为了解某区初中学生对网络游戏的喜好和作业量多少情况,随机抽取了该区500名同学进行了调查,并将调查的情况进行了整理,如下表:
作业量多少 网络游戏的喜好 | 认为作业多 | 认为作业不多 | 合计 |
喜欢网络游戏 | 180 | 90 | 270 |
不喜欢网络游戏 | 80 | 150 | 230 |
根据抽样调查结果,估计该区12000名初中生“不喜欢网络游戏并认为作业不多”的人数是________.