题目内容
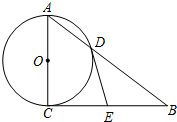 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,E是BC的中点.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,E是BC的中点.(1)求证:DE是⊙O的切线;
(2)过点E作EF⊥DE,交AB于点F.若AC=3,BC=4,求DF的长.
考点:切线的判定,解直角三角形
专题:
分析:(1)连结OD,CD,求出DE=CE=BE,推出∠1+∠3=∠2+∠4,求出∠ACB=∠ODE=90°,根据切线的判定推出即可.
(2)根据勾股定理求出AB=5,解直角三角形得出cosB=
=
,求出DE,推出∠EDF=∠B,解直角三角形求出即可.
(2)根据勾股定理求出AB=5,解直角三角形得出cosB=
| BC |
| AB |
| 4 |
| 5 |
解答:(1)证明:连结OD,CD,
∵AC是直径,
∴∠ADC=90°,
∴∠BDC=180°-∠ADC=90°,
∵E是BC的中点,
∴DE=
BC=CE,
∴∠1=∠2.
∵OC=OD,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,
即∠ACB=∠ODE,
∵∠ACB=90°,
∴∠ODE=90°,
又∵OD是半径,
∴DE是⊙O的切线.
(2)解:在Rt△ABC中,
∵∠ACB=90°,AC=3,BC=4,
∴AB=5,
∴cosB=
=
,
∵E是BC的中点,
∴DE=
BC=BE=2,
∴∠5=∠B,
∴cos∠5=
=
,
∴DF=
DE=
.

∵AC是直径,
∴∠ADC=90°,
∴∠BDC=180°-∠ADC=90°,
∵E是BC的中点,
∴DE=
| 1 |
| 2 |
∴∠1=∠2.
∵OC=OD,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,
即∠ACB=∠ODE,
∵∠ACB=90°,
∴∠ODE=90°,
又∵OD是半径,
∴DE是⊙O的切线.
(2)解:在Rt△ABC中,
∵∠ACB=90°,AC=3,BC=4,
∴AB=5,
∴cosB=
| BC |
| AB |
| 4 |
| 5 |
∵E是BC的中点,
∴DE=
| 1 |
| 2 |

∴∠5=∠B,
∴cos∠5=
| DE |
| DF |
| 4 |
| 5 |
∴DF=
| 5 |
| 4 |
| 5 |
| 2 |
点评:本题考查了等腰三角形的性质,圆周角定理,直角三角形斜边上的中线性质,解直角三角形,切线的判定的应用,注意:经过半径的外端,并且垂直于这条半径的直线是圆的切线.

练习册系列答案
相关题目
 如图,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△AMB;④CD=DN.其中正确的结论是( )
如图,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△AMB;④CD=DN.其中正确的结论是( )| A、①②③ | B、①③④ |
| C、①② | D、②③ |
如图(1)是长方形纸带,∠DEF=α,将纸带沿EF折叠成图(2),再沿BF折叠成图(3),则图(3)中的∠CFE的度数是( )
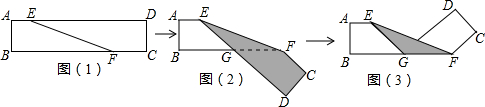

| A、2α |
| B、90°+2α |
| C、180°-2α |
| D、180°-3α |
 如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2-3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.
如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2-3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.
 如图,在△ABC中,D是AB上一点,E是AC上一点,BE与CD相交于点O,∠A=60°,∠ABE=15°,∠ACD=25°,求∠COE的度数.
如图,在△ABC中,D是AB上一点,E是AC上一点,BE与CD相交于点O,∠A=60°,∠ABE=15°,∠ACD=25°,求∠COE的度数.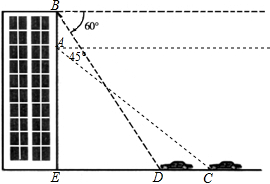 如图,小明在商贸大厦离地面25m高的A处看地面C处汽车,测得俯角为45°,小明上升5m后到B处看到该汽车行驶到D处,测得俯角为60°,若汽车在与该楼的垂直线上行驶,求汽车行驶的距离CD的长.(结果精确到0.1米,参考数据
如图,小明在商贸大厦离地面25m高的A处看地面C处汽车,测得俯角为45°,小明上升5m后到B处看到该汽车行驶到D处,测得俯角为60°,若汽车在与该楼的垂直线上行驶,求汽车行驶的距离CD的长.(结果精确到0.1米,参考数据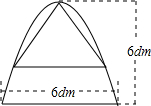 如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形,使其一个顶点与抛物线的顶点重合,另外两个顶点在抛物线上,求这个等边三角形的边长(结果精确到0.1,
如图,有一块铁片下脚料,其外轮廓中的曲线是抛物线的一部分,要裁出一个等边三角形,使其一个顶点与抛物线的顶点重合,另外两个顶点在抛物线上,求这个等边三角形的边长(结果精确到0.1,