Question

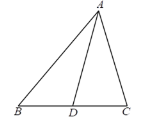
【题目】已知，如图△ABC中，AB＝5，AC＝3，则中线AD的取值范围是（ ）

A. 2＜AD＜8B. 2＜AD＜4C. 1＜AD＜4D. 1＜AD＜8

Answer 1

【答案】C

【解析】

先延长AD到E，且AD=DE，并连接BE，由于∠ADC=∠BDE，AD=DE，利用SAS易证△ADC≌△EDB，从而可得AC=BE，在△ABE中，再利用三角形三边的关系，可得2<AE<8，从而易求1<AD<4．

延长AD到E，使AD=DE，连接BE，

∵AD=DE,∠ADC=∠BDE,BD=DC，

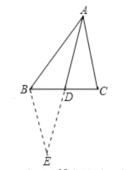
∴△ADC≌△EDB(SAS)

∴BE=AC=3，

在△AEB中，ABBE<AE<AB+BE，

即53<2AD<5+3，

∴1<AD<4，

∴AD的取值范围是1<AD<4，

故选C.