ЬтФПФкШн
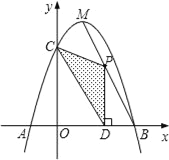
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌOC ODЃЌOC OD ЃЌDC ЕФбгГЄЯпНЛ y жсе§АыжсЩЯЕу B ЃЌЙ§ЕуC зїCA BD НЛ x жсИКАыжсгкЕуA ЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКOAOB
ЃЈ2ЃЉШчЭМ1ЃЌСЌADЃЌзїOM ЁЮACНЛADгкЕуMЃЌЧѓжЄЃК BC 2OM
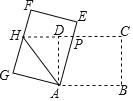
ЃЈ3ЃЉШчЭМ2ЃЌЕуEЮЊOC ЕФбгГЄЯпЩЯвЛЕуЃЌСЌDEЃЌЙ§ЕуDзїDFDEЧвDF DE ЃЌСЌCF НЛ DO ЕФбгГЄЯпгкЕуG ШєOG 4ЃЌЧѓCE ЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉCE=OT=8ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩOCЁЭODЃЌCAЁЭBDжЊЁЯCOD=ЁЯBCA=ЁЯAOB=90ЁуЃЌДгЖјЕУЁЯAOC=ЁЯBODЃЌЁЯOBD=ЁЯOACЃЌНсКЯOC=ODжЄЁїAOCЁеЁїBODПЩЕУД№АИЃЛ
ЃЈ2ЃЉзїANЁЮODЃЌНЛOMбгГЄЯпгкЕуNЃЌЯШжЄЁїBOCЁеЁїOANЕУBC=ONЃЌAN=OC=ODЃЌдйжЄЁїAMNЁеЁїDMOЕУOM=MN=![]() ONЃЌДгЖјЕУжЄЃЛ
ONЃЌДгЖјЕУжЄЃЛ
ЃЈ3ЃЉзїFTЁЭDGЃЌНЛDGбгГЄЯпгкЕуTЃЌЯШжЄЁїFTDЁеЁїDOEЕУFT=OD=OCЃЌDT=OEЃЌдйжЄЁїFTGЁеЁїCOGЕУOT=2OG=8ЃЌИљОнOE=DTЃЌOC=ODПЩЕУCE=OTЃЎ
НтЃКЃЈ1ЃЉЁпOCЁЭODЃЌCAЁЭBDЃЌ
ЁрЁЯCOD=ЁЯBCA=ЁЯAOB=90ЁуЃЌ
ЁрЁЯBOC+ЁЯCOE=90Ёу, ЁЯDOE+ЁЯCOE=90Ёу,
ЁрЁЯBOC=ЁЯDOE,
ЁрЁЯAOC=ЁЯBODЃЌ
ЭЌРэПЩжЄЁЯOBD=ЁЯOACЃЌ
дкЁїAOCКЭЁїBODжаЃЌ
Ёп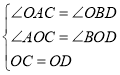 ЃЌ
ЃЌ
ЁрЁїAOCЁеЁїBODЃЈAASЃЉЃЌ
ЁрOA=OBЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЙ§ЕуAзїANЁЮODЃЌНЛOMбгГЄЯпгкЕуNЃЌ

дђЁЯOAN+ЁЯAOD=180ЁуЃЌ
ЁпЁЯAOB=ЁЯCOD=90ЁуЃЌ
ЁрЁЯAOD+ЁЯBOC=180ЁуЃЌ
ЁрЁЯOAN=ЁЯBOCЃЌ
гжЁпOMЁЮACЃЌ
ЁрЁЯAON=ЁЯCAOЃЌ
гЩЃЈ1ЃЉжЊЁЯCAO=ЁЯOBCЃЌ
ЁрЁЯAON=ЁЯOBCЃЌ
гжЁпOA=OBЃЌ
ЁрЁїBOCЁеЁїOANЃЈASAЃЉЃЌ
ЁрBC=ONЃЌAN=OC=ODЃЌ
ЁпANЁЮODЃЌ
ЁрЁЯMAN=ЁЯMDOЃЌЁЯMNA=ЁЯMODЃЌ
ЁрЁїAMNЁеЁїDMOЃЈASAЃЉЃЌ
ЁрOM=MN=![]() ONЃЌМДON=2OMЃЌ
ONЃЌМДON=2OMЃЌ
ЁрBC=2OMЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЙ§ЕуFзїFTЁЭDGЃЌНЛDGбгГЄЯпгкЕуTЃЌ
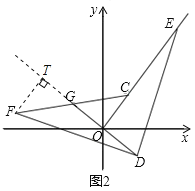
дђЁЯFTD=ЁЯDOE=90ЁуЃЌ
ЁрЁЯODE+ЁЯOED=90ЁуЃЌ
гжЁпDEЁЭDFЃЌ
ЁрЁЯODE+ЁЯFDT=90ЁуЃЌ
ЁрЁЯOED=ЁЯTDFЃЌ
ЁпDE=DFЃЌ
ЁрЁїFTDЁеЁїDOEЃЈAASЃЉЃЌ
ЁрFT=ODЃЌDT=OEЃЌ
ЁпOD=OCЃЌ
ЁрFT=OCЃЌ
ЁпЁЯFTG=ЁЯCOG=90ЁуЃЌЁЯFGT=ЁЯCGOЃЌ
ЁрЁїFTGЁеЁїCOGЃЈAASЃЉЃЌ
ЁрOT=2OG=8ЃЌ
ЁпOE=DTЃЌOC=ODЃЌ
ЁрCE=OT=8ЃЎ