题目内容
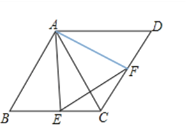
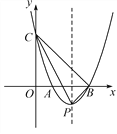
【题目】如图,矩形OABC的顶点A、C分别在x轴和y轴上,顶点B的坐标为(n,2),点E是AB的中点,在OA上取一点D,将△BAD沿BD翻折,点A刚好落在BC边上的F处,BD、EF交于点P
(1)直接写出点E、F的坐标;
(2)若OD=1,求P点的坐标;
(3)动点Q从P点出发,依次经过F,y轴上的点M,x轴上的点N,然后返回到P点:
①若要使Q点运动一周的路径最短,试确定M、N的位置;
②若n=3,求最短路径的四边形PFMN的周长.

【答案】(1)E(n,1);F(n-2,2);(2)点P坐标为(![]() ,
,![]() );(3)①见解析,②
);(3)①见解析,②![]() +
+![]() .
.
【解析】
(1)由翻折知四边形ABFD是正方形,据此得DF=AB=AD=2、OD=CF=BC-BF=n-2,即可得出点F坐标,由E为AB中点可得点E的坐标;
(2)OD=1知n=3,据此得出点B、D、E、F的坐标,分别求得直线BD和直线EF的解析式,联立方程组即可求得BD与EF的交点P的坐标;
(3)①作点F关于y轴的对称点F′、作点P关于x轴的对称点P′,连接F′P′交y轴于点M、交x轴于点N;
②由n=3结合(2)知点P、F及其关于坐标轴的对称点,利用勾股定理求解可得.
(1)∵B(n,2),
∴AB=OC=2、OA=BC=n,
由翻折知△DAB≌△DFB,
∴∠DAB=∠DFB=90°、BA=BF=2,
∵∠ABF=90°,
∴四边形ABFD是正方形,
∴DF=AB=AD=2,
∴OD=CF=BC-BF=n-2,
则F(n-2,2),
∵E为AB中点,
∴AE=BE=1,
∴E(n,1);
(2)若OD=1,则n-2=1,即n=3,
∴B(3,2)、D(1,0)、E(3,1)、F(1,2),
设BD所在直线解析式为y=kx+b,
将点B(3,2)、D(1,0)代入,得:
![]() ,
,
解得:![]() ,
,
∴BD所在直线解析式为y=x-1;
设EF所在直线解析式为y=mx+n,
将E(3,1)、F(1,2)代入,得:![]() ,
,
解得: ,
,
∴EF所在直线解析式为y=-![]() x+
x+![]() ;
;
由 可得
可得![]() ,
,
所以点P坐标为(![]() ,
,![]() );
);
(3)①如图所示,作点F关于y轴的对称点F′、作点P关于x轴的对称点P′,连接F′P′交y轴于点M、交x轴于点N,

②若n=3,由(2)知P(![]() ,
,![]() )、F(1,2),
)、F(1,2),
则F′(-1,2)、P′(![]() ,-
,-![]() ),
),
∴PF=![]() =
=![]() ,P′F′=
,P′F′=![]() =
=![]() ,
,
∴C四边形PFMN=![]() +
+![]() .
.

【题目】某自行车厂一周计划生产150辆自行车,平均每天生产辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正、减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比生产量最少的一天多生产 辆;
(3)该厂实行计划工资制,每辆车![]() 元,超额完成任务每辆奖
元,超额完成任务每辆奖![]() 元,少生产一辆扣
元,少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少?
【题目】在一次活动中,主办方共准备了3600盆甲种花和2900盆乙种花,计划用甲、乙两种花搭造出A、B两种园艺造型共50个,搭造要求的花盆数如下表所示:
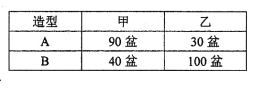
请问符合要求的搭造方案有几种?请写出具体的方案。
【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为![]() ~
~![]() 的产品为合格〉.随机各抽取了20个祥品迸行检测.过程如下:
的产品为合格〉.随机各抽取了20个祥品迸行检测.过程如下:
收集数据(单位:![]() ):
):
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.
整理数据:
组别频数 | 165.5~170.5 | 170.5~175.5 | 175.5~180.5 | 180.5~185.5 | 185.5~190.5 | 190.5~195.5 |
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 | 1 | 2 |
|
| 2 | 0 |
分析数据:
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
应用数据;
(1)计算甲车间样品的合格率.
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息.请判断哪个车间生产的新产品更好.并说明理由.