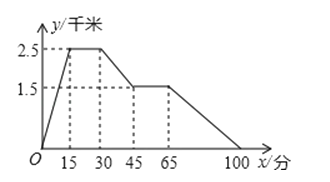
题目内容
【题目】在□ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
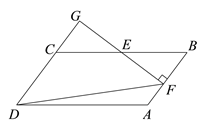
(1)求证:GD=GF.
(2)已知BC=10, ![]() .求 CD的长.
.求 CD的长.
【答案】(1)证明见解析;
(2)CD长为5
【解析】试题分析:(1)由ABCD是平行四边形得:AB∥CD,又因为EF⊥AB,所以∠ DGF=∠GFB=90°,在△DGF中,求得∠FDG=∠DFG=45° ,再根据等角对等边得到GD=GF;
(2)由![]() 且
且 ![]() 得:GF=8,又由 BC=10 ,点E 是BC中点,则CE=5,由ABCD是平行四边形 得: ∠ GCE=∠EBF,则△EBF≌△ECG,所以GE=4 ,在在 Rt△CGE 中
得:GF=8,又由 BC=10 ,点E 是BC中点,则CE=5,由ABCD是平行四边形 得: ∠ GCE=∠EBF,则△EBF≌△ECG,所以GE=4 ,在在 Rt△CGE 中 ![]() 所以CG=3, CD=8-3=5;
所以CG=3, CD=8-3=5;
试题解析:
(1)证明:
∵EF⊥AB,
∴∠GFB=90°
∵ABCD是平行四边形
∴AB∥CD, ∠ DGF=∠GFB=90°
在△DGF中,已知∠FDG=45°
∴∠DFG=45°
∴∠FDG=∠DFG
∴GD=GF
(2)解:由(1)得![]() 又
又 ![]()
∴![]()
∴GF=8
∵ BC=10 ,点E 是BC中点
∴CE=5
∵ABCD是平行四边形
∴ ∠ GCE=∠EBF
在△EBF和△ECG中
∠ EFB=∠ECG=90°
CE=EB=5
∴△EBF≌△ECG
∴GE=4
在 Rt△CGE 中 ![]()
∴CG=3
∴CD=8-3=5

练习册系列答案
相关题目