题目内容
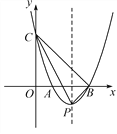
【题目】如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点(-1,8)并与x轴交于A,B两点,且点B坐标为(3,0).
(1)求抛物线的表达式;
(2)若抛物线与y轴交于点C,顶点为点P,求△CPB的面积.
【答案】(1)抛物线的表达式为y=x2-4x+3;(2)△CPB的面积为3
【解析】试题分析: (1)将已知点的坐标代入二次函数的解析式,解关于![]() 的二元一次方程组即可;
的二元一次方程组即可;
(2)过点P作PH⊥Y轴于点H,过点B作BM∥y轴交直线PH于点M,过点C作CN⊥y轴叫直线BM于点N,则S△CPB=S矩形CHMNS△CHPS△PMBS△CNB由此计算即可;
试题解析: (1)∵抛物线![]() 经过点(1,8)与点B(3,0),
经过点(1,8)与点B(3,0),
∴![]() 解得:
解得:![]()
∴抛物线的解析式为:![]()
(2)![]()
∴P(2,1)
过点P作PH⊥Y轴于点H,过点B作BM∥y轴交直线PH于点M,过点C作CN⊥y轴叫直线BM于点N,如下图所示:

S△CPB=S矩形CHMNS△CHPS△PMBS△CNB![]()
即:△CPB的面积为3.

练习册系列答案
相关题目