题目内容
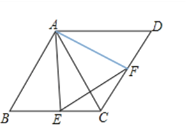
【题目】菱形ABCD中,∠B=60°,点E,F分别是BC,CD上的两个动点,且始终保持∠AEF=60°.
(1)试判断△AEF的形状并说明理由;
(2)若菱形的边长为2,求△ECF周长的最小值.
【答案】(1)△AEF是等边三角形,理由详见解析;(2)2+![]()
【解析】
(1)先根据四边形ABCD是菱形判断出△ABC的形状,再由ASA定理得出△AGE≌△ECF,故可得出AE=AF,由此可得出结论;
(2)根据垂线段最短可知当AE⊥BC时△ECF周长最小,由直角三角形的性质求出AE的长,故可得出结论.
解:(1)△AEF是等边三角形,理由是:
∵四边形ABCD是菱形,
∴AB=BC
∵∠B=60°.
∴△ABC是等边三角形,
在AB上截取BG=BE,则△BGE是等边三角形
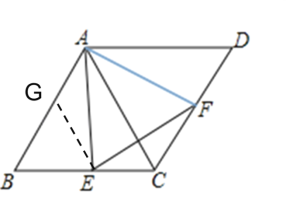
∴AG=AB-BG=BC-BE=EC,
∵∠AEC=∠BAE+∠B=∠AEF+∠FEC,又因为∠B=∠AEF=60°
∴∠BAE=∠CEF.
在△AGE与△ECF中,
∠AGE=∠ECF=120°,AG=EC,∠GAE=∠CEF
∴△AGE≌△ECF(ASA),
∴AE=EF.
∵∠AEF=60°,
∴△AEF是等边三角形.
(2)由(1)知△AEF是等边三角形,△AGE≌△ECF
所以CF=GE=BE,CF+EC=BC=定值=2
∵垂线段最短,
∴当AE⊥BC时,AE=EF最小,此时△ECF周长最小、
∵BC=2,∠B=60°,
∴AE=![]() ,
,
△ECF周长的最小值=2+![]() .
.

【题目】为极大地满足人民生活的需求,丰富市场供应,某区农村温棚设施农业迅速发展,温棚种植面积在不断扩大.在耕地上培成一行一行的长方形土埂,按顺序间隔种植不同农作物的方法叫分垄间隔套种.科学研究表明:在塑料温棚中分垄间隔套种高、矮不同的蔬菜和水果(同一种紧挨在一起种植不超过两垄),可增加它们的光合作用,提高单位面积的产量和经济效益.
现有一个种植总面积为540 m2的长方形塑料温棚,分垄间隔套种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物的总垄数不低于10垄,又不超过14垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
占地面积(m2/垄) | 产量(千克/垄) | 利润(元/千克) | |
西红柿 | 30 | 160 | 1.1 |
草莓 | 15 | 50 | 1.6 |
(1)若设草莓共种植了![]() 垄,通过计算说明共有几种种植方案,分别是哪几种;
垄,通过计算说明共有几种种植方案,分别是哪几种;
(2)在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?