题目内容

（五005•枣庄）已知抛物线y=（1-0）x五+8x+b的图象的的部分八图所示，抛物的顶点在第的象限，且经过点0（0，-7）和点B．
（1）求0的取值范围；
（五）若O0=五OB，求抛物线的解析式．
（5）由图可知，b=-7．（5分）
故抛物线为y=（5-a）x4+9x-7．
又因抛物线的顶点在第一象限，开9向z，
所以抛物线与x轴有两个不同的交点．
∴
5-a＜口
94-8(5-a)(-7)＞口
，
解之，得5＜a＜
49
7
．（9分）
即a的取值范围是5＜a＜
49
7
．（6分）

（4）设B（x5，口），
由OA=4口B，
得7=4x5，即x5=
7
4
．（7分）
由于x5=
7
4
，方程（5-a）x4+9x-7=口的一个根，
∴（5-a）（
7
4
）4+9×
7
4
-7=口
∴a=
59
7
．（9分）
故所求所抛物线解析式为y=-
54
7
x4+9x-7．（5口分）
练习册系列答案
相关题目
已知二次函数y=x2-mx+m-2．
（1）求证：无论m为任何实数，该二次函数的图象与x轴都有两个交点；
（2）当该二次函数的图象经过点（3，6）时，求二次函数的解析式；
（3）将直线y=x向下平移2个单位长度后与（2）中的抛物线交于A、B两点（点A在点B的左边），一个动点P自A点出发，先到达抛物线的对称轴上的某点E，再到达x轴上的某点F，最后运动到点B．求使点P运动的总路径最短的点E、点F的坐标，并求出这个最短总路径的长．
已知抛物线y=-
1
2
x2+bx+4上有不同的两点E（k+3，-k2+1）和F（-k-1，-k2+1）．
（1）求抛物线的解析式；
（2）如图，抛物线y=-
1
2
x2+bx+4与x轴和y轴的正半轴分别交于点A和B，M为AB的中点，∠PMQ在AB的同侧以M为中心旋转，且∠PMQ=45°，MP交y轴于点C，MQ交x轴于点D．设AD的长为m（m＞0），BC的长为n，求n和m之间的函数关系式；
（3）当m，n为何值时，∠PMQ的边过点F？
如图，二次函数y1=x2+bx+c的图象与x轴交于A、B两点，与y轴交于点C，且点B的坐标为（1，0），点C的坐标为（0，-3），一次函数y2=mx+n的图象过点A、C．
（1）求二次函数的解析式；
（2）求二次函数的图象与x轴的另一个交点A的坐标；
（3）根据图象写出y2＜y1时，x的取值范围．
如图，已知抛物线y=-x2+mx+3与x轴的一个交点A（3，0）．
（1）你一定能分别求出这条抛物线与x轴的另一个交点B及与y轴的交点C的坐标，试试看；
（2）设抛物线的顶点为D，请在图中画出抛物线的草图．若点E（-2，n）在直线BC上，试判断E点是否在经过D点的反比例函数的图象上，把你的判断过程写出来；
（3）请设法求出tan∠DAC的值．
在平面直角坐标系xOy中，抛物线y=-x2-（m-1）x+m2-6交x轴负半轴于点A，交y轴正半轴于点B（0，3），顶点C位于第二象限，连接AB，AC，BC．
（1）求抛物线的解析式；
（2）点D是y轴正半轴上一点，且在B点上方，若∠DCB=∠CAB，请你猜想并证明CD与AC的位置关系；
（3）设与△AOB重合的△EFG从△AOB的位置出发，沿x轴负方向平移t个单位长度（0＜t≤3）时，△EFG与△ABC重叠部分的面积为S，求S与t之间的函数关系式．
如图，以O为原点的直角坐标系中，A点的坐标为（0，3），直线x=-3交x轴于点B，P为线段AB上一动点，作直线PC⊥PO，交于直线x=-3于点C．过P点作直线MN平行于x轴，交y轴于M，交直线x=-3于点N．
（1）当点C在第二象限时，求证：△OPM≌△PCN；
（2）设AP长为m，以P、O、B、C为顶点的四边形的面积为S，请求出S与M之间的函数关系式，并写出自变量m的取值范围；
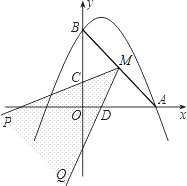
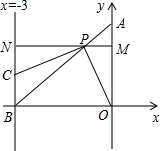（3）当点P在线段AB上移动时，点C也随之在直线x=-3上移动，△PBC是否可能成为等腰三角形？如果可能，求出所有能使△PBC成为等腰三角形的点P的坐标；如果不可能，请说明理由．
廊桥是我国古老的文化遗产．如图，是某座抛物线型的廊桥示意图，已知抛物线的函数表达式为y=-
1
40
x2+10，为保护廊桥的安全，在该抛物线上距水面AB高为8米的点E，F处要安装两盏警示灯，则这两盏灯的水平距离EF是______米．（精确到1米）
如图：已知抛物线y=
1
4
x2+
3
2
x-4与x轴交于A，B两点，与y轴交于点C，O为坐标原点．
（1）求A，B，C三点的坐标；
（2）已知矩形DEFG的一条边DE在AB上，顶点F，G分别在线段BC，AC上，设OD=m，矩形DEFG的面积为S，求S与m的函数关系式，并指出m的取值范围；
（3）当矩形DEFG的面积S取最大值时，连接对角线DF并延长至点M，使FM=
2
5
DF．试探究此时点M是否在抛物线上，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网