题目内容
若直线y=-| 4 | 3 |
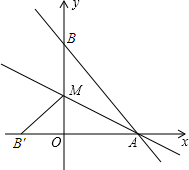
(1)求A、B两点的坐标;
(2)若坐标原点为O,对于一个长与宽分别为OB与OA的矩形C,请设计另一个矩形,使得它的周长和面积恰好都是矩形C的周长和面积的2倍.
分析:(1)根据直线解析式直接求出A、B两点的坐标;
(2)原矩形长、宽分别为3,4,则周长为14,面积为12,设新矩形长、宽分别为a,b,则2a+2b=28,ab=24,解方程组求a、b即可.
(2)原矩形长、宽分别为3,4,则周长为14,面积为12,设新矩形长、宽分别为a,b,则2a+2b=28,ab=24,解方程组求a、b即可.
解答:解:(1)由直线y=-
x+4,令y=0得x=3,令x=0得y=4,
∴A(3,0),B(0,4);
(2)由(1)可知,原矩形长、宽分别为3,4,
∴周长为14,面积为12,
设新矩形长、宽分别为a,b,
则2a+2b=28,ab=24,
解方程组
,
得a=12,b=2,
∴另外一个矩形的长、宽分别为12,2.
| 4 |
| 3 |
∴A(3,0),B(0,4);
(2)由(1)可知,原矩形长、宽分别为3,4,
∴周长为14,面积为12,
设新矩形长、宽分别为a,b,
则2a+2b=28,ab=24,
解方程组
|
得a=12,b=2,
∴另外一个矩形的长、宽分别为12,2.
点评:本题考查了一次函数的综合运用.关键是根据解析式求出原矩形的长、宽,设另外一个矩形的长、宽,根据题意列方程组求解.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
若直线y=
x-4与x轴正方向的夹角为α,则cosα等于( )
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 (2013•河西区一模)直线y=-
(2013•河西区一模)直线y=-
