Question

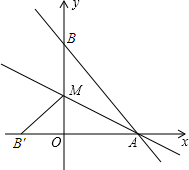（2013•河西区一模）直线y=-

4

3

x+8与x轴、y轴分别交于点A和点B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处．
（Ⅰ）线段AB的长度为

10

；
（Ⅱ）△B′OM的周长为

12

；
（Ⅲ）求点M的坐标．

Answer 1

分析：（Ⅰ）首先求出直线与坐标轴交点坐标，进而得出BO，AO的长，再利用勾股定理求出AB的长；
（Ⅱ）根据翻折变换的性质得出BM=B′M，AB=AB′=10，进而求出△B′OM的周长为：MB′+MO+OB′；
（Ⅲ）根据勾股定理直接求出MO的长，即可得出答案．

解答：解：（Ⅰ）∵直线y=-

4

3

x+8与x轴、y轴分别交于点A和点B，
∴y=0时，x=6，则A点坐标为：（6，0），
x=0时，y=8，则B点坐标为：（0，8）；
∴BO=8，AO=6，
∴AB=

82+62

=10；

（Ⅱ）∵将△ABM沿AM折叠，点B恰好落在x轴上的点B′处，
∴BM=B′M，AB=AB′=10，
∴B′M+OM=BO=8，
OB′=AB′-OA=10-6=4，
∴△B′OM的周长为：MB′+MO+OB′=8+4=12；

（Ⅲ）设MO=x，则MB=MB′=8-x，
在Rt△OMB′中，
OM²+OB′²=B′M²，
∴x²+4²=（8-x）²，
解得：x=3，
故M点坐标为：（0，3）．
故答案为：10；12．

点评：此题主要考查了翻折变换的性质以及勾股定理的应用和一次函数与坐标轴交点求法等知识，根据已知得出A，B两点坐标以及利用翻折变换的性质得出BM=B′M，AB=AB′是解题关键．