Question

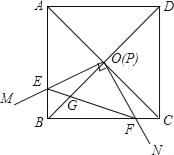
【题目】如图，边长为1的正方形ABCD的对角线AC，BD相交于点O，直角∠MPN的顶点P与点O重合，直角边PM，PN分别与OA，OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是_____.

（1）EF=OE；（2）S四边形OEBF：S正方形ABCD=1：4；（3）在旋转过程中，当△BEF与△COF的面积之和最大时，AE=；（4）OGBD=AE2+CF2.

Answer 1

【答案】（1）（2）（4）

【解析】

（1）由四边形ABCD是正方形，直角∠MPN，易证得△BOE≌△COF（ASA），则可证得结论；（2）由（1）易证得S四边形OEBF=S△BOC=S正方形ABCD，则可证得结论； （3）首先设AE=x，则BE=CF=1﹣x，BF=x，继而表示出△BEF与△COF的面积之和，然后利用二次函数的最值问题，求得答案；（4）易证得△OEG∽△OBE，然后由相似三角形的对应边成比例，证得OGOB=OE2，再利用OB与BD的关系，OE与EF的关系，即可证得结论．

∵四边形ABCD是正方形，

∴OB=OC，∠OBE=∠OCF=45°，∠BOC=90°，

∴∠BOF+∠COF=90°，

∵∠EOF=90°，

∴∠BOF+∠COE=90°，

∴∠BOE=∠COF，

在△BOE和△COF中，

，

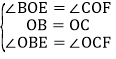∴△BOE≌△COF（ASA），

∴OE=OF，BE=CF，

∴EF=OE；故（1）正确；

∵S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=S正方形ABCD，

∴S四边形OEBF：S正方形ABCD=1：4；故（2）正确；

过点O作OH⊥BC，

∵BC=1，

∴OH=BC=，

设AE=x，则BE=CF=1-x，BF=x，

∴S△BEF+S△COF=BEBF+CFOH=x（1-x）+（1-x）×=-（x-）2+，

∵a=-<0，

∴当x=时，S△BEF+S△COF最大；

即在旋转过程中，当△BEF与△COF的面积之和最大时，AE=；故（3）错误；

∵∠EOG=∠BOE，∠OEG=∠OBE=45°，

∴△OEG∽△OBE，

∴OE：OB=OG：OE，

∴OGOB=OE2，

∵OB=BD，OE=EF，

∴OGBD=EF2，

∵在△BEF中，EF2=BE2+BF2，

∴EF2=AE2+CF2，

∴OGBD=AE2+CF2．故（4）正确，

综上所述：（1）（2）（4）正确，

故答案为：（1）（2）（4）