题目内容
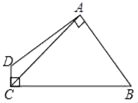
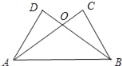
【题目】如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
求证:△OAB是等腰三角形.
【答案】详见解析.
【解析】
利用HL定理得出△ABD≌BAC即可得出∠DBA=∠CAB,再利用等腰三角形的判定得出即可.
证明: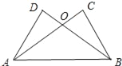
∵AC⊥BC,BD⊥AD
∴∠D=∠C=90°,
在Rt△ABD和Rt△BAC中,
![]() ,
,
∴Rt△ABD≌Rt△BAC(HL),
∴∠DBA=∠CAB,
∴OA=OB,
即△OAB是等腰三角形.
另外一种证法:
证明:∵AC⊥BC,BD⊥AD
∴∠D=∠C=90°
在Rt△ABD和Rt△BAC中
![]()
∴Rt△ABD≌Rt△BAC(HL)
∴AD=BC,
在△AOD和△BOC中
![]() ,
,
∴△AOD≌△BOC(AAS),
∴OA=OB,
即△OAB是等腰三角形.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目