题目内容
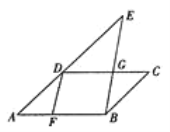
【题目】如图,△ABC的周长为1,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.

【答案】![]()
【解析】
根据E、F、G分别为AB、AC、BC的中点,可以判断EF、FG、EG为三角形中位线,利用中位线定理求出EF、FG、EG与BC、AB、CA的长度关系即可求得△EFG的周长是△ABC周长的一半,△A'B'C'的周长是△EFG的周长的一半,以此类推,可以求得第n个三角形的周长.
∵如图,△ABC的周长为1,E、F、G分别为AB、AC、BC的中点,∴EF、FG、EG为三角形中位线,∴EF![]() BC,EG
BC,EG![]() AC,FG
AC,FG![]() AB,∴EF+FG+EG
AB,∴EF+FG+EG![]() (BC+AC+AB)
(BC+AC+AB)![]() ,即△EFG的周长是△ABC周长的一半.
,即△EFG的周长是△ABC周长的一半.
同理,△A'B'C'的周长是△EFG的周长的一半,即△A'B'C'的周长为![]() 1
1![]() =
=![]() .
.
以此类推,第n个小三角形的周长是第一个三角形周长的1×(![]() )n﹣1=
)n﹣1=![]() .
.
故答案为:![]() .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品每天的利润为y元。
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?最大利润是多少?
(3)该商品在销售过程中,共有多少天每天的销售利润不低于4800元?请直接写出结果。