Question

【题目】如图，ABCD 中，G是CD上一点，BG交AD延长线于E，AF=CG，．

（1） 求证：DF=BG；

（2）求的度数．

Answer 1

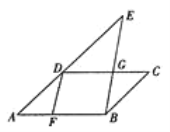
【答案】（1）证明见解析；（2）100°

【解析】

（1）一组对边平行且相等的四边形是平行四边形，在本题中可知存在这一关系的是DG和BF，所以四边形DFBG为平行四边形，因此DF=BG；

（2）两直线平行，同位角相等，在本题中用到了两次此性质，可得出所求结论．

（1）∵四边形ABCD是平行四边形，

∴AB=DC，又∵AF=CG，∴AB﹣AF=DC﹣CG，即GD=BF．

又DG∥BF，∴四边形DFBG是平行四边形，∴DF=BG．

（2）∵四边形DFBG是平行四边形，∴DF∥GB，∴∠GBF=∠AFD．

同理可得∠GBF=∠DGE，∴∠AFD=∠DGE=100°．