题目内容
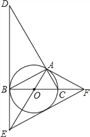
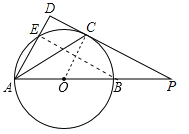
【题目】如图，已知AB为⊙O的直径，点E在⊙O上，∠EAB的平分线交⊙O于点C，过点C作AE的垂线，垂足为D，直线DC与AB的延长线交于点P．
（1）判断直线PC与⊙O的位置关系，并说明理由；
（2）若tan∠P=
，AD=6，求线段AE的长．
【答案】（1）PC是⊙O的切线；（2）
【解析】试题分析：（1）结论：PC是⊙O的切线．只要证明OC∥AD，推出∠OCP=∠D=90°，即可．
（2）由OC∥AD，推出
，即
，解得r=
，由BE∥PD，AE=ABsin∠ABE=ABsin∠P，由此计算即可．
试题解析：解：（1）结论：PC是⊙O的切线．理由如下：
连接OC．∵AC平分∠EAB，∴∠EAC=∠CAB．又∵∠CAB=∠ACO，∴∠EAC=∠OCA，∴OC∥AD．∵AD⊥PD，∴∠OCP=∠D=90°，∴PC是⊙O的切线．
（2）连接BE．在Rt△ADP中，∠ADP=90°，AD=6，tan∠P=
，∴PD=8，AP=10，设半径为r．∵OC∥AD，∴
，即
，解得r=
．∵AB是直径，∴∠AEB=∠D=90°，∴BE∥PD，∴AE=ABsin∠ABE=ABsin∠P=
×
=
．
练习册系列答案
相关题目
