题目内容
【题目】如图,在河对岸有一棵大树 A,在河岸 B 点测得 A 在北偏东 60°方向上,向东前进 200m 到达 C 点,测得 A 在北偏东 30°方向上,求河的宽度(精确到 0.1m).参考数据 ![]() ≈1.414,
≈1.414,![]() ≈1.732.
≈1.732.
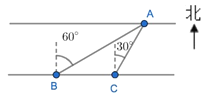
【答案】河的宽度为173.2米.
【解析】
过点A作AD⊥直线BC,垂足为点D,在Rt△ABD和Rt△ACD中,通过解直角三角形可求出BD,CD的长,结合BC=BDCD=200,即可求出AD的长.
解:过点A作AD⊥直线BC,垂足为点D,如图所示.
由题意可知:∠BAD=60°,∠CAD=30°,
在Rt△ABD中,tan∠BAD=![]() ,
,
∴BD=ADtan60°=![]() ;
;
在Rt△ACD中,tan∠CAD=![]() ,
,
∴CD=ADtan30°=![]() .
.
∴BC=BDCD=![]() -
-![]() =200,
=200,
∴AD=![]() .
.
∴河的宽度为173.2米.


练习册系列答案
相关题目