题目内容
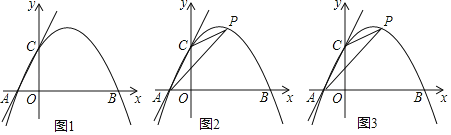
【题目】在平面直角坐标系xOy中抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
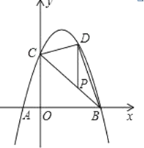
(1)求抛物线的表达式;
(2)如图,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BCD的面积最大时,求点P的坐标.
【答案】(1)y=﹣x2+2x+3;(2)当a=![]() 时,△BDC的面积最大,此时P点坐标为:(
时,△BDC的面积最大,此时P点坐标为:(![]() ,
,![]() );
);
【解析】
(1)利用待定系数法求解即可;
(2)先求出点B的坐标,即可得出直线BC的解析式,设P(a,3﹣a),则D(a,﹣a2+2a+3),即可得PD=﹣a2+3a,再根据三角形的面积公式即可得出S△BDC![]() ,从而可得当a=
,从而可得当a=![]() 时,△BDC的面积最大,得出此时P点坐标.
时,△BDC的面积最大,得出此时P点坐标.
(1)∵y=﹣x2+bx+c经过点A(﹣1,0),C(0,3)
∴-1-b+c=0,c=3,
解得:b=2,c=3,
∴抛物线解析式为y=﹣x2+2x+3;
(2)在y=﹣x2+2x+3中,
当y=0时,x1=﹣1,x2=3,
即B(3,0),
设直线BC的解析式为y=kx+m,
∴3k+m=0,m=3,
∴直线BC的解析式为y=﹣x+3,
设P(a,3﹣a),则D(a,﹣a2+2a+3),
∴PD=(﹣a2+2a+3)﹣(3﹣a)
=﹣a2+3a,
∴S△BDC=![]() PD·OB
PD·OB
=![]() PD
PD
=﹣![]() (a﹣
(a﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当a=![]() 时,△BDC的面积最大,此时P点坐标为:(
时,△BDC的面积最大,此时P点坐标为:(![]() ,
,![]() );
);

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目