题目内容
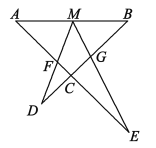
【题目】如图,点M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B,且DM交AC于点F,ME交BC于点G.写出图中的所有相似三角形,并选择一对加以证明.
【答案】△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM,证明见解析.
【解析】
根据相似三角形的判定定理可以直接写出图中有3对相似三角形;可以利用相似三角形的判定定理两组角对应相等的两个三角形相似来证明△AMF∽△BGM.
图中的相似三角形有:△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM.
以下证明△AMF∽△BGM.
∵∠AFM=∠DME+∠E(外角定理),∠DME=∠A=∠B(已知),∴∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B,∴△AMF∽△BGM.

练习册系列答案
相关题目