Question

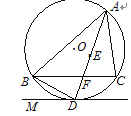
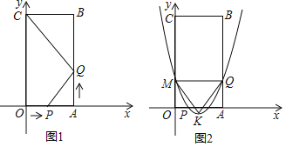
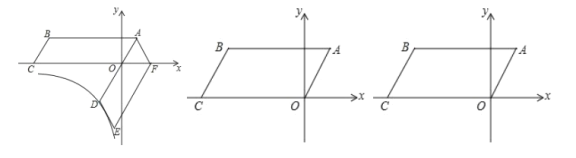
【题目】如图，在平面直角坐标系中，四边形为平行四边形，为坐标原点，，将平行四边形绕点逆时针旋转得到平行四边形，点在的延长线上，点落在轴正半轴上．

(1)证明:是等边三角形:

(2)平行四边形绕点逆时针旋转度．的对应线段为,点的对应点为

①直线与轴交于点,若为等腰三角形，求点的坐标:

②对角线在旋转过程中设点坐标为，当点到轴的距离大于或等于时，求的范围．

Answer 1

【答案】（1）见解析（2）①P（0, ）或（0, -4）②-8≤m≤-或≤m≤12

【解析】

(1)根据A点坐标求出∠AOF=60°，再根据旋转的特点得到AO=AF，故可求解；

（2）①设P（0,a）根据等腰三角形的性质分AP=OP和AO=OP，分别求出P点坐标即可；

②分旋转过程中在第三象限时到轴的距离等于与旋转到第四象限时到轴的距离等于，再求出当旋转180°时的坐标，即可得到m的取值．

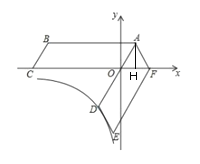
（1）如图，过A点作AH⊥x轴，

∵

∴OH=2,AH=2

∴AO=

故AO=2OH

∴∠OAH=30°

∴∠AOF=90°-∠OAH=60°

∵旋转

∴AO=AF

∴△AOF是等边三角形；

（2）①设P（0,a）

∵是等腰三角形

当AP=OP时，（2-0）2+（2-a）2=a2

解得a=

∴P（0, ）

当AO=OP时，OP= AO=4

∴P（0, -4）

故为等腰三角形时，求点的坐标是（0, ）或（0, -4）；

②旋转过程中点的对应点为，

当开始旋转，至到轴的距离等于时，m的取值为-8≤m≤-；

当旋转到第四象限，到轴的距离等于时，m=

当旋转180°时，设C’的坐标为(x,y)

∵C、关于A点对称，

∴

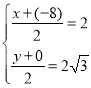
解得

∴（12，）

∴m的取值为≤m≤12，

综上，当点到轴的距离大于或等于时，求的范围是-8≤m≤-或≤m≤12．