Question

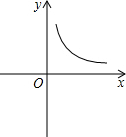
如图，A、B是双曲线y=

2

x

上任意两点，过A、B两点分别作y轴的垂线，垂足分别为C、D，且C、D的纵坐标分别为3和1．连接AB，直线OB、OA分别交图象于点E、F，则△EOF的面积是______．

Answer 1

过点B向x轴作垂线，垂足是G，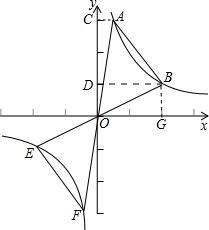
由已知可得：点A的纵坐标为3，则由双曲线y=

2

x

得A的横坐标为

2

3

，
点B的纵向坐标为1，则横坐标为2，
∴矩形BDOG的面积为2×1=2，
∴所以S_△AOB=S_矩形BDOG+S_梯形ACDB-S_△AOC-S_△BOG=2+

1

2

×（2+

2

3

）×（3-1）-

1

2

×3×

2

3

-

1

2

×2×1=

8

3

，
根据双曲线的对称性，所以得△EOF的面积为

8

3

，
故答案为：

8

3

．