题目内容
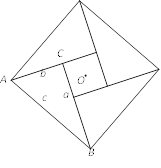
【题目】如图,△ABC内接于⊙O,AB=AC,AD是⊙O的切线,BD∥AC,BD交⊙O于点E,连接AE,则下列结论:①∠DAE=∠BAC;②AE=BE;③AD=AE;④四边形ACBD是平行四边形,其中不正确的是__________.(只填序号)
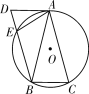
【答案】②
【解析】
利用弦切角与圆周角关系可知∠DAE=∠ABE;BD∥AC可知∠ABE=∠BAC,得证①成立,利用圆内接四边形知识和三角形内角和180°,证明相关角的等量关系,证明线段的数量与位置关系.
∵AD是⊙O的切线,
∴∠DAE=∠ABD.
∵BD∥AC,
∴∠CAB=∠ABD,
∴∠DAE=∠CAB,故①正确;
∵四边形AEBC内接于⊙O,
∴∠AED=∠ACB.
∴△ADE∽△ABC,
∴![]() ,∠ABC=∠ADE,
,∠ABC=∠ADE,
由AB=AC,得AD=AE,故③正确;
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ADE=∠ACB,
∴DE∥AC,
∴∠DBA=∠BAC,
∴在△BAD和△ABC中,∠ADE=∠ACB,∠DBA=∠BAC,AB=AB,
∴△BAD≌△ABC,
∴AC=BD,
∴四边形ACBD是平行四边形,故④正确.
②无法得到,故错误.
故答案为:②

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目