Question

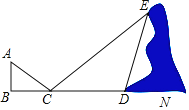
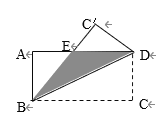
【题目】如图，矩形ABCD中，AB＝3，BC＝4，将该矩形沿对角线BD折叠，则图中阴影部分的面积是多少？

Answer 1

【答案】

【解析】

由矩形与折叠的性质，易证得△BDE是等腰三角形，然后设ED＝EB＝x，在Rt△ABE中，由AB2＋AE2＝BE2，可得方程：32＋（4x）2＝x2，解此方程即可求得DE的长，继而求得阴影部分的面积．

∵四边形ABCD是矩形，

∴∠A＝90°，AD∥BC，AD＝BC＝4，

∴∠EDB＝∠DBC，

由折叠的性质可得：∠EBD＝∠DBC，

∴∠EBD＝∠EDB，

∴EB＝ED，

设ED＝EB＝x，则AE＝ADED＝4x，

在Rt△ABE中，AB2＋AE2＝BE2，

即32＋（4x）2＝x2，

解得：x＝，

即DE＝，

∴S阴影＝S△BDE＝DEAB＝××3＝．

答：图中阴影部分的面积是．