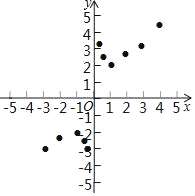��Ŀ����
����Ŀ������������ö����Ͱ�����Щ�����ɫ���������������ѧ�������������飺ÿ������һ��������ɫ��Ż�ҡ�ȣ��ظ���������������õ��������ݣ�
����Ĵ���n | 100 | 200 | 300 | 500 | 800 | 1000 |
��������Ĵ���m | 38 | 79 | 121 | 196 | 322 | 398 |
���������Ƶ�� | 0.380 | 0.395 | 0.403 | 0.392 | 0.403 | 0.398 |
��1�����ݱ������ݹ��ƣ��Ӻ�������һ�����ǰ���ĸ�����_____����ȷ��0.01����
��2�������к����������5ö��ijͬѧ�������Żص���������������״ͼ������������������ɫ��ͬ�ĸ��ʣ�
���𰸡�(1)0.60;(2)������.
��������
��1�������ظ������������Ƶ�ʿ��Թ�������ĸ��ʣ��ݴ���⣻
��2������״ͼ�г����еȿ��ܽ�������ҵ����������Ľ���������ݸ��ʹ�ʽ���ɵã�
�⣺��1�����ݱ������ݹ��ƴӺ�������һ�����ǰ���ĸ�����1��0.40��0.60��
�ʴ�Ϊ��0.60��
��2���ɣ�1����֪������ĸ���Ϊ5��0.40��2�������ĸ���Ϊ3��
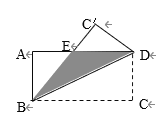
����״ͼ���£�
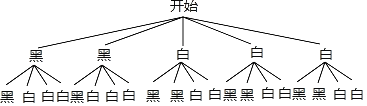
�ɱ���֪�����еȿ��ܽ������20�������
������������ɫ��ͬ����12�ֽ����
������������ɫ��ͬ�ĸ���Ϊ![]() ��
��

����Ŀ��С������ѧϰ�����ľ��飬�Ժ���y=x+![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
������С����̽�����̣��벹��������
��1������y=x+![]() ���Ա���x��ȡֵ��Χ��_____��
���Ա���x��ȡֵ��Χ��_____��
��2���±��г���y��x�ļ����Ӧֵ����д��m��n��ֵ��m=_____��n=_____��
x | �� | ��3 | ��2 | ��1 | �� | �� |
|
| 1 | 2 | 3 | 4 | �� |
y | �� | �� | �� | ��2 | �� | �� | m |
| 2 |
| n |
| �� |
��3����ͼ����ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣬��������ĵ㣬�����ú�����ͼ����
��4����Ϻ�����ͼ������ɣ�
�ٵ�y=��![]() ʱ��x=_____��
ʱ��x=_____��
��д���ú�����һ������_____��
��������x+![]() =t����������ȵ�ʵ��������t��ȡֵ��Χ��_____��
=t����������ȵ�ʵ��������t��ȡֵ��Χ��_____��