题目内容
【题目】在Rt△ABC中,∠ACB=90°,tan∠BAC=![]() . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
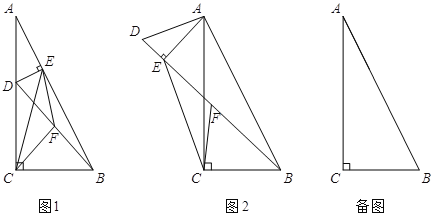
(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设![]() ,则k= ;
,则k= ;
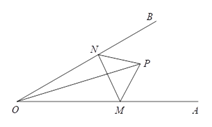
(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
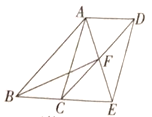
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
【答案】(1)k=1(2)证明![]() ,则可得
,则可得![]() . (3)当点D在靠近点C的
. (3)当点D在靠近点C的
三等分点时,线段CF的长度取得最大值为![]()
【解析】试题分析:解:(1)k=1; .
(2)如图2,过点C作CE的垂线交BD于点G,设BD与AC的交点为Q.
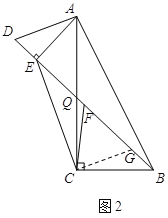
由题意,tan∠BAC=![]() ,
,
∴![]() .
.
∵D、E、B三点共线,
∴AE⊥DB.
∵∠BQC=∠AQD,∠ACB=90°,
∴∠QBC=∠EAQ.
∵∠ECA+∠ACG=90°,∠BCG+∠ACG=90°,
∴∠ECA=∠BCG.
∴![]() .
.
∴![]() .
.
∴GB=DE.
∵F是BD中点,
∴F是EG中点.
在![]() 中,
中, ![]() ,
,
∴![]() . . .
. . .
(3)情况1:如图,当AD= ![]() 时,取AB的中点M,连结MF和CM,
时,取AB的中点M,连结MF和CM,
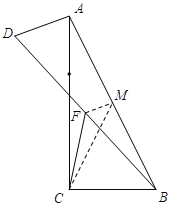
∵∠ACB=90°, tan∠BAC=![]() ,且BC= 6,
,且BC= 6,
∴AC=12,AB=![]() .
.
∵M为AB中点,∴CM=![]() ,
,
∵AD= ![]() ,
,
∴AD=![]() .
.
∵M为AB中点,F为BD中点,
∴FM= ![]() = 2.
= 2.
∴当且仅当M、F、C三点共线且M在线段CF上时CF最大,此时CF=CM+FM=![]() .
.
情况2:如图,当AD= ![]() 时,取AB的中点M,连结MF和CM,
时,取AB的中点M,连结MF和CM,
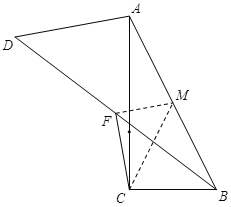
类似于情况1,可知CF的最大值为![]() .
.
. 6分
综合情况1与情况2,可知当点D在靠近点C的
三等分点时,线段CF的长度取得最大值为![]()

练习册系列答案
相关题目