题目内容
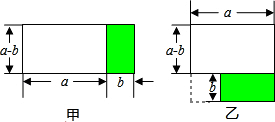
将图甲中阴影部分的小长方形变换到图乙位置，根据两个图形的面积关系可以得到一个关于a、b的恒等式为（ ）
| A．（a-b）2=a2-2ab+b2 | B．（a+b）2=a2+2ab+b2 |
| C．（a+b）（a-b）=a2-b2 | D．a（a-b）=a2-ab |
图甲面积=（a-b）（a+b），
图乙面积=a（a-b+b）-b×b=a2-b2，
∵两图形的面积相等，
∴关于a、b的恒等式为：（a+b）（a-b）=a2-b2．
故选C．
图乙面积=a（a-b+b）-b×b=a2-b2，
∵两图形的面积相等，
∴关于a、b的恒等式为：（a+b）（a-b）=a2-b2．
故选C．
练习册系列答案
阅读快车系列答案
相关题目
