题目内容
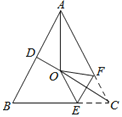
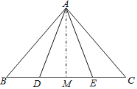
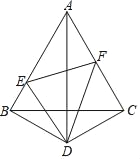
【题目】如图所示,D是等边三角形ABC外一点,DB=DC,∠BDC=120°,点E,F分别在AB,AC上.
(1)求证:AD是BC的垂直平分线.
(2)若ED平分∠BEF,求证:FD平分∠EFC.
(3)在(2)的条件下,求∠EDF的度数.
【答案】(1)见解析;(2)见解析;(3)∠EDF=60°.
【解析】
(1)求出AB=AC,BD=DC,根据线段垂直平分线性质求出即可;
(2)过D作DM⊥EF,连接AD,求出AD平分∠BAC,求出∠ABC=∠ACB=60°,求出BD=DM,BD=DC,推出DM=DC即可;
(3)求出DB=DM,DM=DC,∠EBD=∠EMD=90°,证出△EBD≌△EMD,推出∠BDE=∠EDM,同理∠CDF=∠FDM,进而得出2∠EDF=∠BDC=120°.
(1)∵△ABC是等边三角形,
∴AB=AC,
∴A在BC的垂直平分线上,
∵BD=DC,
∴D在BC的垂直平分线上,
∴AD是BC的垂直平分线
(2)过D作DM⊥EF,连接AD,
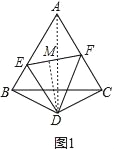
∵AD是BC的垂直平分线,
∴AD平分∠BAC,
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵BD=DC,∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠ABD=∠ACD=90°,
∴DB⊥AB,DC⊥AC,
∵DM⊥EF,ED平分∠BEF,AD平分∠BAC,
∴BD=DM,BD=DC,
∴DM=DC,
∴FD平分∠EFC;
(3)如图,
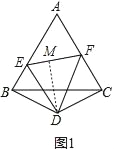
∵DE平分∠BEF,DB⊥AB,DM⊥EF,DF平分∠CFE,
∴DB=DM,DM=DC,∠EBD=∠EMD=90°,
在△EBD和△EMD中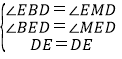 ,
,
∴△EBD≌△EMD,
∴∠BDE=∠EDM,
同理∠CDF=∠FDM,
∴2∠EDF=∠BDC=180°﹣30°﹣30°=120°,
∴∠EDF=60°.

 阅读快车系列答案
阅读快车系列答案【题目】下表中有两种移动电话计费方式:
月使用费 | 主叫限定时间(分钟) | 主叫超时费(元/分钟) | 被叫 | |
方式一 | 65 | 160 | 0.20 | 免费 |
方式二 | 100 | 380 | 0.25 | 免费 |
(月使用费固定收;主叫不超过限定的时间不再收费,主叫超过限定时间的部分加收超时费;被叫免费)
(1)若张聪某月主叫通话时间为200分钟,则他按方式一计费需____元,按方式二计费需____
元;李华某月按方式二计费需107元,则李华该月主叫通话时间为_____分钟;
(2)是否存在某主叫通话时间![]() (分钟),按方式一和方式二的计费相等?若存在,请求出
(分钟),按方式一和方式二的计费相等?若存在,请求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(3)直接写出当月主叫通话时间![]() (分钟)满足什么条件时,选择方式一省钱。
(分钟)满足什么条件时,选择方式一省钱。