��Ŀ����
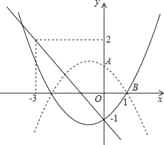
����Ŀ����ƽ��ֱ������ϵxOy�У����κ���y=mx2����m+n��x+n��m��0����ͼ����y�������ύ��A�㣮
��1����֤���ö��κ�����ͼ����x������������㣻
��2����ö��κ�����ͼ����x��������������Ҳ�Ľ���Ϊ��B������ABO=45������ֱ��AB����ƽ��2����λ�õ�ֱ��l����ֱ��l�Ľ���ʽ��
��3���ڣ�2���������£���M��p��q��Ϊ���κ���ͼ���ϵ�һ�����㣬����3��p��0ʱ����M����x��ĶԳƵ㶼��ֱ��l���·�����m��ȡֵ��Χ��
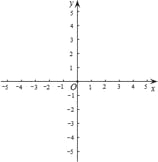
���𰸡���1���ö��κ�����ͼ����������������㣻��2��y=��x��1����3��m��ȡֵ��ΧΪ����![]() ��m��0��
��m��0��
�������������������1��ֱ�����ø����б�ʽ�������ȫƽ����ʽ������ķ��Ž����ó��𰸣�
��2���������B��A�����꣬�������ֱ��AB�Ľ���ʽ��������ƽ�ƹ��ɵó��𰸣�
��3�����ݵ���3��p��0ʱ����M����x��ĶԳƵ㶼��ֱ��l���·�����p=0ʱ��q=1����p=��3ʱ��q=12m+4�����ͼ���֪������12m+4����2�����ɵó�m��ȡֵ��Χ��
�����������1����mx2����m+n��x+n=0������=��m+n��2��4mn=��m��n��2��
�����κ���ͼ����y�������ύ��A�㣬��A��0��n������n��0��
����m��0����m��n��0�����=��m��n��2��0��
���ö��κ�����ͼ����������������㣻
��2����mx2����m+n��x+n=0����ã�x1=1��x2=![]() ���ɣ�1����
���ɣ�1����![]() ��0����B������Ϊ��1��0����
��0����B��������1��0����
������ABO=45����
����A��0��1������n=1��
������ֱ��AB�Ľ���ʽΪ��y=��x+1��
������ƽ��2����λ�ɵõ�ֱ��l��y=��x��1��
��3���ɣ�2���ö��κ����Ľ���ʽΪ��y=mx2����m+1��x+1��
��M��p��q�� Ϊ���κ���ͼ���ϵ�һ�����㣬
��q=mp2����m+1��p+1��
����M������ĶԳƵ�M��������Ϊ��p����q����
��M�����ڶ��κ���y=��m2+��m+1��x��1�ϣ�
������3��p��0ʱ����M����x��ĶԳƵ㶼��ֱ��l���·���
��p=0ʱ��q=1����p=��3ʱ��q=12m+4��
���ͼ���֪������12m+4����2����ã�m����![]() ��
��
��m��ȡֵ��ΧΪ����![]() ��m��0��
��m��0��