题目内容
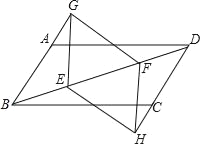
【题目】如图,在ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.
求证:(1)△BEG≌△DFH;
(2)四边形GEHF是平行四边形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)利用平行四边形的性质得出BG=DH,进而利用SAS得出△BEG≌△DFH;
(2)利用全等三角形的性质得出∠GEF=∠HFB,进而得出答案.
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥DC,
∴∠ABE=∠CDF,
∵AG=CH,
∴BG=DH,
在△BEG和△DFH中,
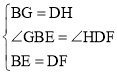 ,
,
∴△BEG≌△DFH(SAS);
(2)∵△BEG≌△DFH(SAS),
∴∠BEG=∠DFH,EG=FH,
∴∠GEF=∠HFB,
∴GE∥FH,
∴四边形GEHF是平行四边形.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
【题目】小林同学积极参加体育锻炼,天天坚持跑步,他每天以1000m为标准,超过的记作正数,不足的记作负数.下表是一周内小明跑步情况的记录(单位:m):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
跑步情况(m) | +420 | +460 | -100 | -210 | -330 | +200 | -240 |
(1)星期三小林跑了_____米
(2)小林在跑得最少的一天跑了______米?跑得最多的一天比最少的一天多跑了_____米?
(3)若小林跑步的平均速度为240米/分,求本周内小明用于跑步的时间.