题目内容
有一边长为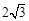
的正三角形，则它的外接圆的面积为（）
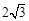的正三角形，则它的外接圆的面积为（）A． | B． | C． | D． |
C
分析：正三角形的边长为
，可得其外接圆的半径为2 ÷cos30°× 
=2，故其面积为4π．
解：∵正三角形的边长为，可得其外接圆的半径为2 ÷cos30°× =2，故其面积为4π
故选C．
点评：本题考查等边三角形的性质与运用，其三边相等，三个内角相等，均为60度．
，可得其外接圆的半径为2 ÷cos30°× =2，故其面积为4π．解：∵正三角形的边长为
，可得其外接圆的半径为2 ÷cos30°× =2，故其面积为4π故选C．
点评：本题考查等边三角形的性质与运用，其三边相等，三个内角相等，均为60度．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
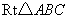的两直角边的长分别为6cm和8cm，则它的外接圆的半径为__ __cm.
