题目内容
【题目】已知直线y=﹣![]() x+2分别交x、y轴于点A、B,点C为线段OA的中点,动点P从坐标原点出发,以2个单位长度/秒的速度向终点A运动,动点Q从点C出发,以
x+2分别交x、y轴于点A、B,点C为线段OA的中点,动点P从坐标原点出发,以2个单位长度/秒的速度向终点A运动,动点Q从点C出发,以![]() 个单位长度/秒的速度向终点B运动.过点Q作QM∥AB交x轴于点M,动点P、Q同时出发,其中一个点到达终点,另一个点也停止运动,设点P运动的时间为t秒,PM的长为y个单位长度.
个单位长度/秒的速度向终点B运动.过点Q作QM∥AB交x轴于点M,动点P、Q同时出发,其中一个点到达终点,另一个点也停止运动,设点P运动的时间为t秒,PM的长为y个单位长度.
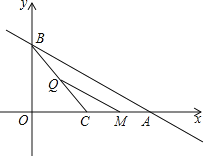
(1)∠BCO= °;
(2)求y关于t的函数关系式及自变量t的取值范围;
(3)是否存在时间t,使得以PC为直径的⊙D与直线QM相切?若存在,求t的值;不存在,说明理由.
【答案】(1)45;(2)y=2﹣t(0≤t≤2)(3)当t=1﹣![]() 或t=1+
或t=1+![]() 时,以PC为直径的⊙D与直线QM相切
时,以PC为直径的⊙D与直线QM相切
【解析】
试题分析:(1)先分别求得点A和点B的坐标,从而得到点C的坐标,从而得到OB=OC,于是可求得∠BCO的度数;
(2)先由相似三角形的性质得到CM的长,然后依据PM=CO+CM﹣OP可求得y与t的函数关系式;
(3)当点P在点C的左边时,可求得DM=1,由tan∠NMD=![]() ,可求得DN=
,可求得DN=![]() ,然后可求得DC=1﹣t,从而可求得t的值;当点P在点C的右侧时,可求得DC=t﹣1,DN=
,然后可求得DC=1﹣t,从而可求得t的值;当点P在点C的右侧时,可求得DC=t﹣1,DN=![]() ,从而可求得t的值.
,从而可求得t的值.
解:(1)∵令y=0得﹣![]() x+2=0,解得:x=4,
x+2=0,解得:x=4,
∴A(0,4).
∴OA=4.
∵点C为线段OA的中点,
∴OC=2.
∵令x=0得:y=2,
∴B(0,2).
∴OB=2.
∴OB=OC.
又∵∠BOC=90°,
∴∠BCO=45°.
故答案为:45.
(2)如图1所示:

∵OB=CO=2,∠BOC=90°,
∴BC=![]() OB=2
OB=2![]() .
.
∵OA=4,OC=2,
∴AC=2.
设点P和点Q的运动时间为t,则OP=2t,QP=![]() t.
t.
∵QM∥AB,
∴![]() ,即
,即![]() ,解得CM=t.
,解得CM=t.
∴PM=CO+CM﹣OP=2+t﹣2t=2﹣t(0≤t≤2).
∴y与t的函数关系是为y=2﹣t(0≤t≤2).
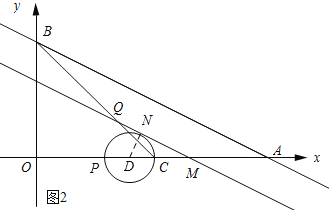
(3)如图2所示:设N为切线,连接DN.
∵OP=2t,OC=2,
∴PC=2﹣2t.
∴PD=DC=1﹣t.
∴DM=PM﹣PD=2﹣t﹣(1﹣t)=1.
∵MQ是圆D的切线,
∴DN⊥QM.
∵OB=2,OA=4,
∴tan∠BAO=![]() .
.
∵QM∥AB,
∴tan∠NMP=![]() .
.
∴DN=![]() DM=
DM=![]() .
.
∴1﹣t=![]() ,解得:t=1
,解得:t=1![]() .
.
如图3所示:设N为切线,连接DN.

∵OP=2t,OC=2,
∴PC=2t﹣2.
∴DC=DP=t﹣1.
∴DM=t﹣1+2﹣t=1.
∴DN=![]() .
.
∴t﹣1=![]() ,解得:t=1+
,解得:t=1+![]() .
.
综上所述,当t=1﹣![]() 或t=1+
或t=1+![]() 时,以PC为直径的⊙D与直线QM相切.
时,以PC为直径的⊙D与直线QM相切.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案