题目内容
【题目】如图，△ABC中，AB＝24，BC＝26，CA＝14．顺次连接△ABC各边中点，得到△A1B1C1；再顺次连接△A1B1C1各边中点，得到△A2B2C2…如此进行下去，得到
，则△A8B8C8的周长为（ ）
A.1B.
C.
D.
【答案】C
【解析】
根据三角形中位线定理求出△A1B1C1的周长，根据计算总结规律，根据规律解答.
根据三角形中位线定理求出△A1B1C1的周长，根据计算结果总结规律，根据规律解答．
解：∵A1、C1分别为AB、AC的中点，
∴A1C1＝BC＝13，
同理，A1B1＝
AC＝7，B1C1＝AB＝12，
∴△A1B1C1的周长＝7+12+13＝32，
∴△A1B1C1的周长＝△ABC的周长×，
则△A2B2C2的周长＝△A1B1C1的周长×＝△ABC的周长×（）2，
……
∴△A8B8C8的周长＝△ABC的周长×（）8＝64×
＝
，
故选：C．
练习册系列答案
相关题目
【题目】某学校开展了“好读书、读好书”的课外阅读活动，为了解同学们的读书情况，从全校随机抽取了
名学生，并统计它们平均每天的课外阅读时间（单位：
），然后利用所得数据绘制成如下不完整的统计图表.
课外阅读时间频数分布表
课外阅读时间 | 频数 | 百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
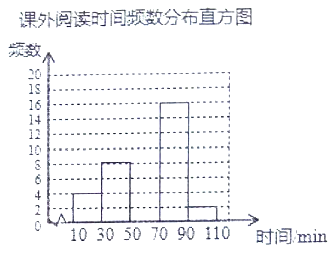
请根据图表中提供的信息回答下列问题：
（1）填空：
__________，
__________；
（2）将频数分布直方图补充完整；
（3）若全校有
名学生，估计该校有多少名学生平均每天的课外阅读时间不少于
？
