题目内容
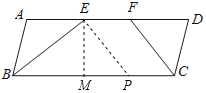
【题目】如图,ABCD中,BE平分∠ABC交AD于E,CF平分∠BCD交AD于F.
(1)求证:AF=DE;
(2)若E为AD的三等分点(靠近A点),BE=8,CF=6,求直线AD与BC之间的距离.

【答案】(1)见解析 (2)4.8
【解析】
(1)证出∠AEB=∠ABE,∠DFC=∠DCF,得出AE=AB,DF=DC,得出AE=DF,进而得出结论;
(2)作EM⊥BC于M,证出AE=EF=DF,过点E作EP∥CF交BC于P,则∠BPE=∠BCF,四边形CFEP是平行四边形,得出EP=CF=6,证出∠BEP=90°,由勾股定理求出![]() ,由面积法求出
,由面积法求出![]() 即可.
即可.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,AD∥BC,
∴∠AEB=∠CBE,∠DFC=∠BCF,
∵BE平分∠ABC,CF平分∠BCD.
∴∠ABE=∠CBE,∠DCF=∠BCF,
∴∠AEB=∠ABE,∠DFC=∠DCF,
∴AE=AB,DF=DC,
∴AE=DF,
∴AE+EF=DF+EF,
即AF=DE;
(2)解:作EM⊥BC于M,如图所示:
由(1)得:AE=DF,
∵E为AD的三等分点,
∴AE=EF=DF,
过点E作EP∥CF交BC于P,
则∠BPE=∠BCF,四边形CFEP是平行四边形,
∴EP=CF=6,
∵AB∥DC,
∴∠ABC+∠DCB=180°,
∵BE平分∠ABC,CF平分∠BCD.
∴∠ABE=∠CBE,∠DCF=∠BCF,
∴∠CBE+∠BCF=90°,
∴∠CBE+∠BPE=90°,
∴∠BEP=90°,
∴![]() ,
,
∴![]() ,
,
即AD与BC之间的距离为4.8.

练习册系列答案
相关题目








